Slides
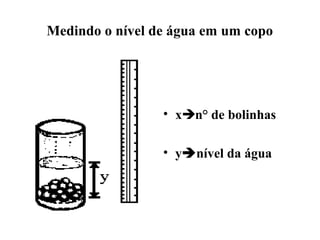
- 1. Medindo o nível de água em um copo • xn° de bolinhas • ynível da água
- 2. • O nível da água no copo é função do número de bolinhas de gude que são colocadas dentro do copo. Considerando o número de bolinhas como a variável independente e o nível de água como variável dependente, determine sua equação e seu respectivo gráfico.
- 3. • Um copo cilíndrico com água; • Bolinhas de gude(35) • Uma régua; • Folhas de papel milimetrado. Materiais utilizados
- 4. Procedimento • colocar água no copo até atingir uma determinada altura a qual será designado o nível zero; • coloque as bolinhas de gude no copo com água (5 de cada vez) e anote numa tabela o nível que está a água; • construir, na folha de papel milimetrado, o gráfico (número de bolinhas x nível da água) a partir dos valores que você obteve.
- 5. Tabela dos dados coletados x(n° de bolinhas) 0 5 10 15 20 25 30 35 y(mm) nível da água 0 16 33 49 65 82 98 114
- 6. 1 1 )( )( + + ∆ ∆ i i x yx (n° de bolinhas) y(mm) nível da água 0 5 10 15 20 25 30 35 0 16 33 49 65 82 98 114 — 3,2 3,4 3,2 3,2 3,4 3,2 3,2
- 7. OBS: Devido ao fato de possíveis erros de medida vamos considerar a razão como constante e adotar essa taxa de variação igual a 3,2. Observando dois valores quaisquer da tabela, é possível perceber que a razão entre os valores da função e da variável é uma constante. Na terceira coluna determina-se quanto y variou em relação à x. Para se obter a equação e o gráfico correspondente, a partir de um conjunto de dados calcula-se inicialmente a taxa de variação pelo quociente.
- 8. a = taxa de variação variação na função = 16 – 0 = 16 variação na variável = 5 – 0 = 5 16 : 5 = 3,2 Esse coeficiente pode ser calculado, usando quaisquer dois outros pontos da tabela, isto significa que a razão entre os valores da função e da variável é uma constante, o que de fato caracteriza uma reta.
- 9. Substituindo o coeficiente na equação geral, tem-se: f(x) = 3,2x + b Para encontrar b, atribui-se um ponto arbitrário da tabela. Por exemplo: 49 = 3,2 . 15 + b 49 = 48 + b 49 – 48 = b b = 1
- 10. Logo, a equação que descreve a função é dada por: f(x) = 3,2x + 1
- 11. Gráfico dos dados coletados: Número de bolinhas X Nível da água(mm) 0 20 40 60 80 100 120 0 10 20 30 40 Número de bolinhas Níveldaágua(mm)
- 12. Gráfico obtido através da função 12,3 += xy