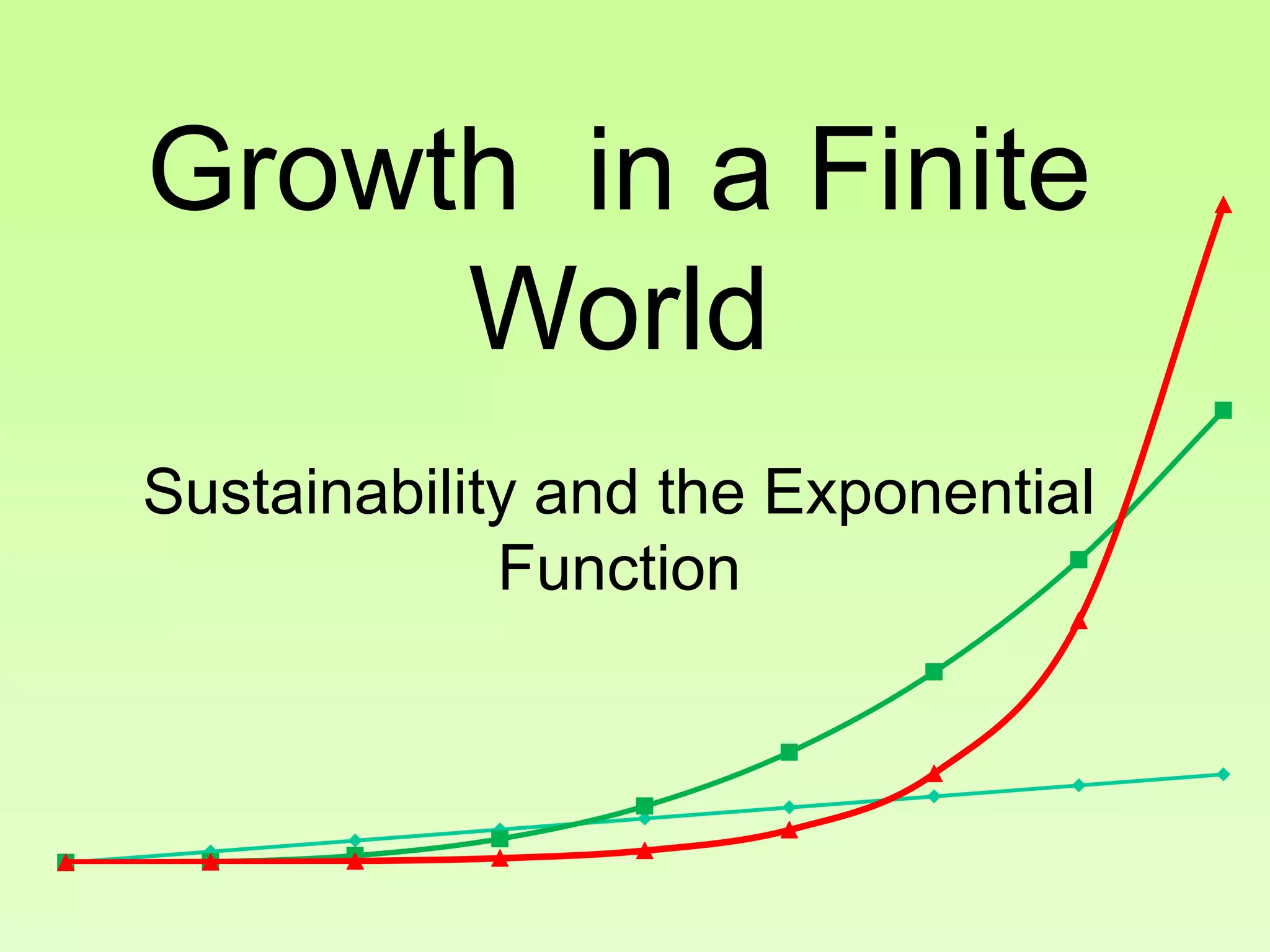
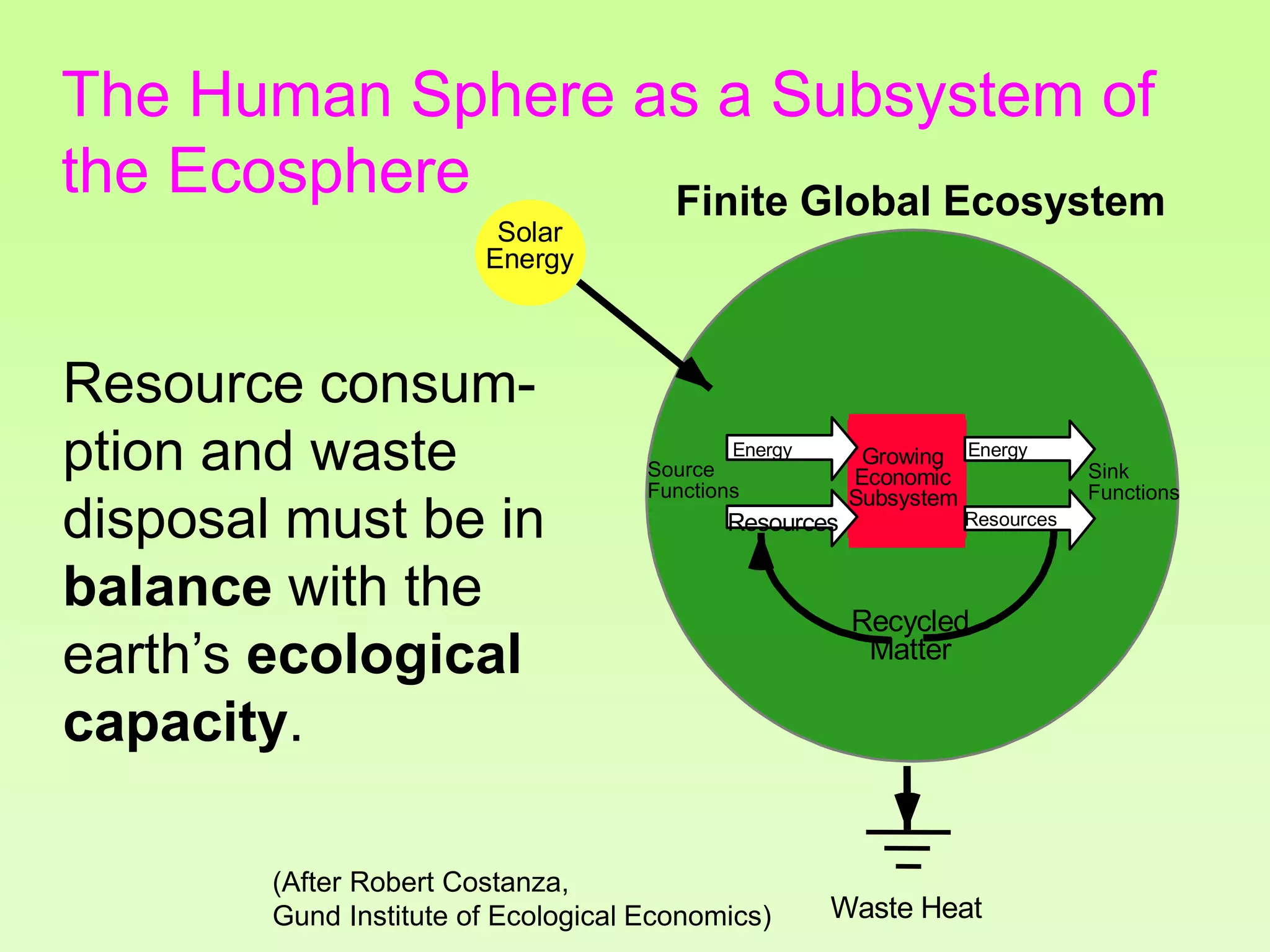
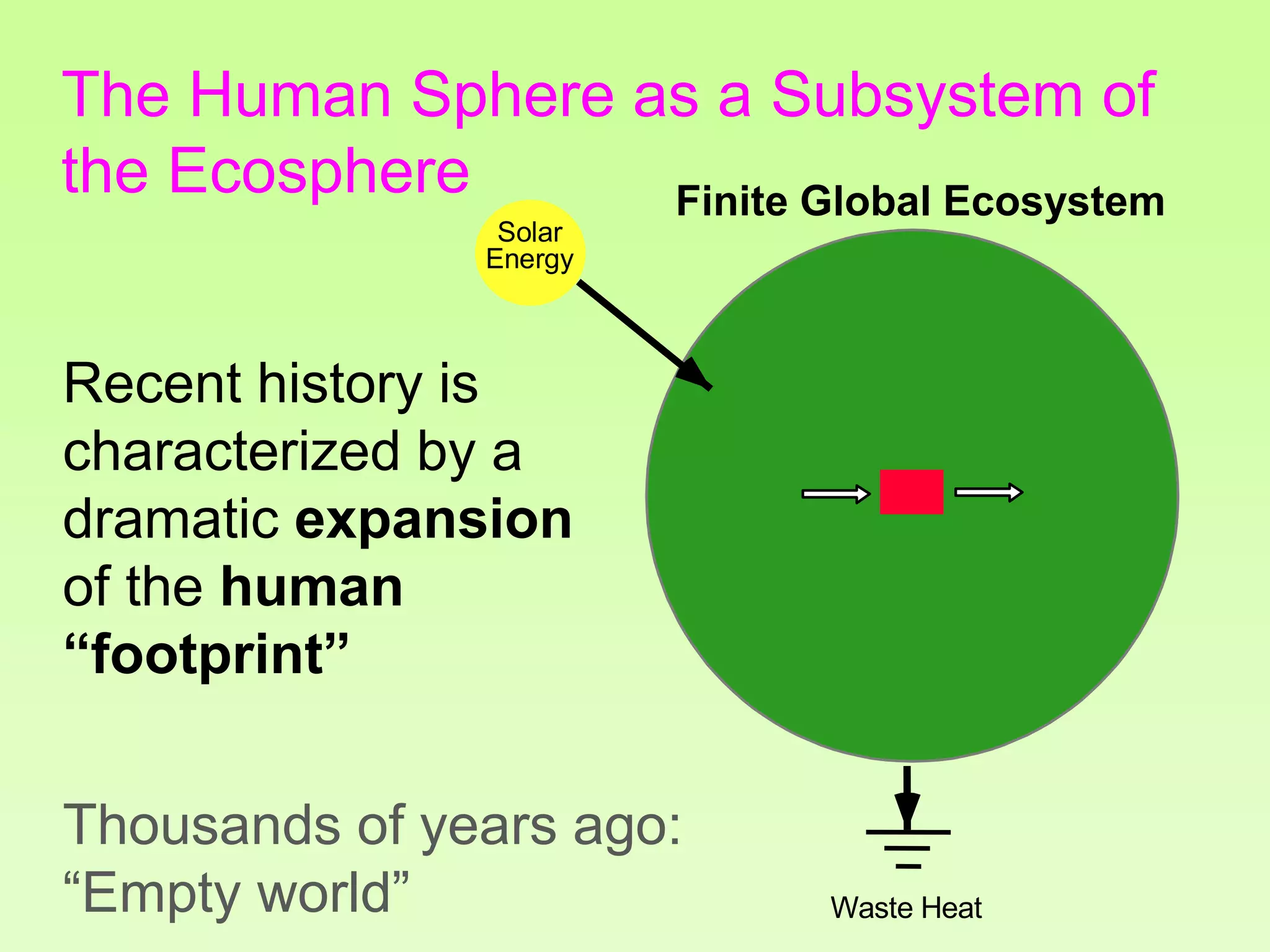
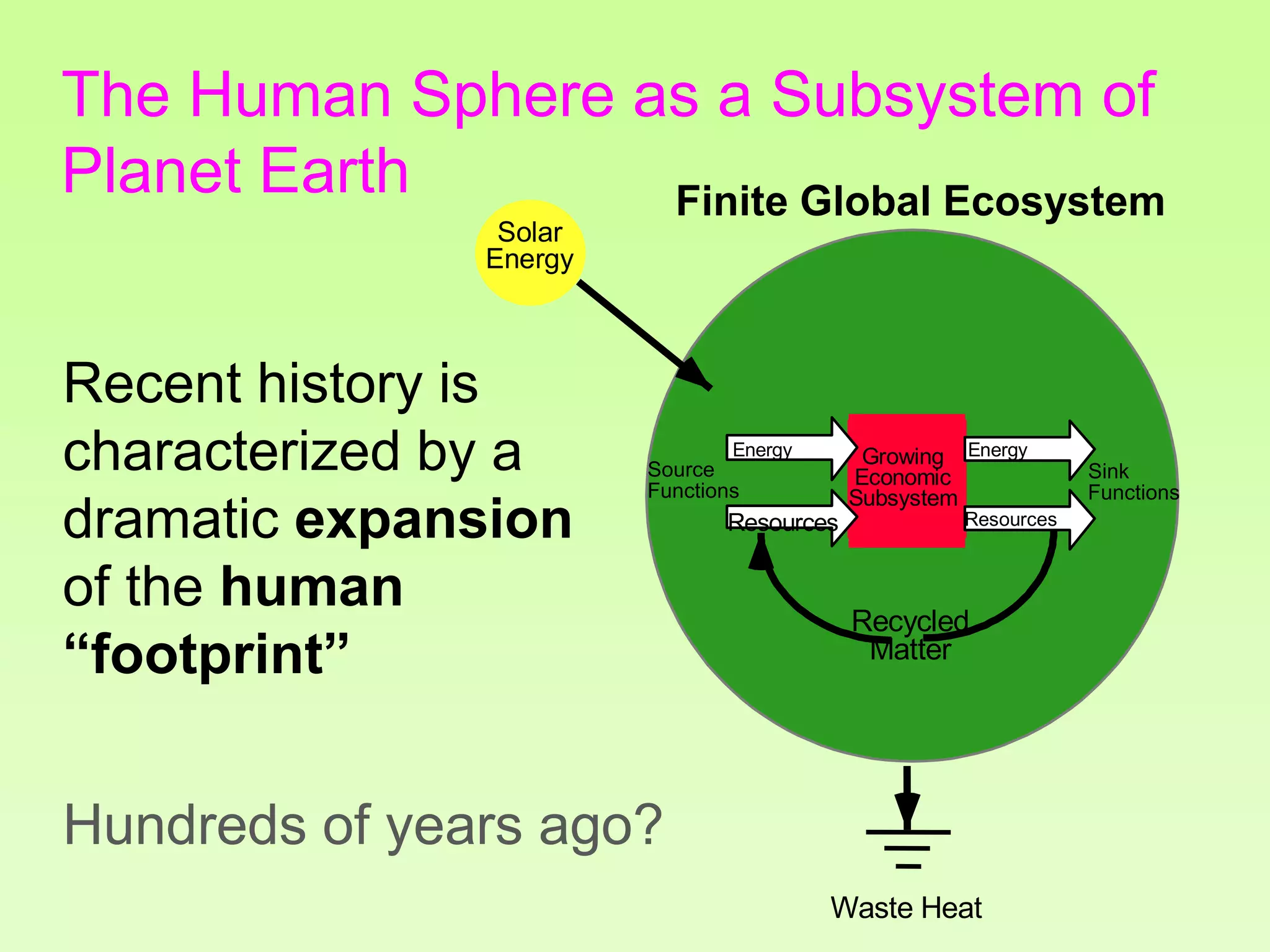
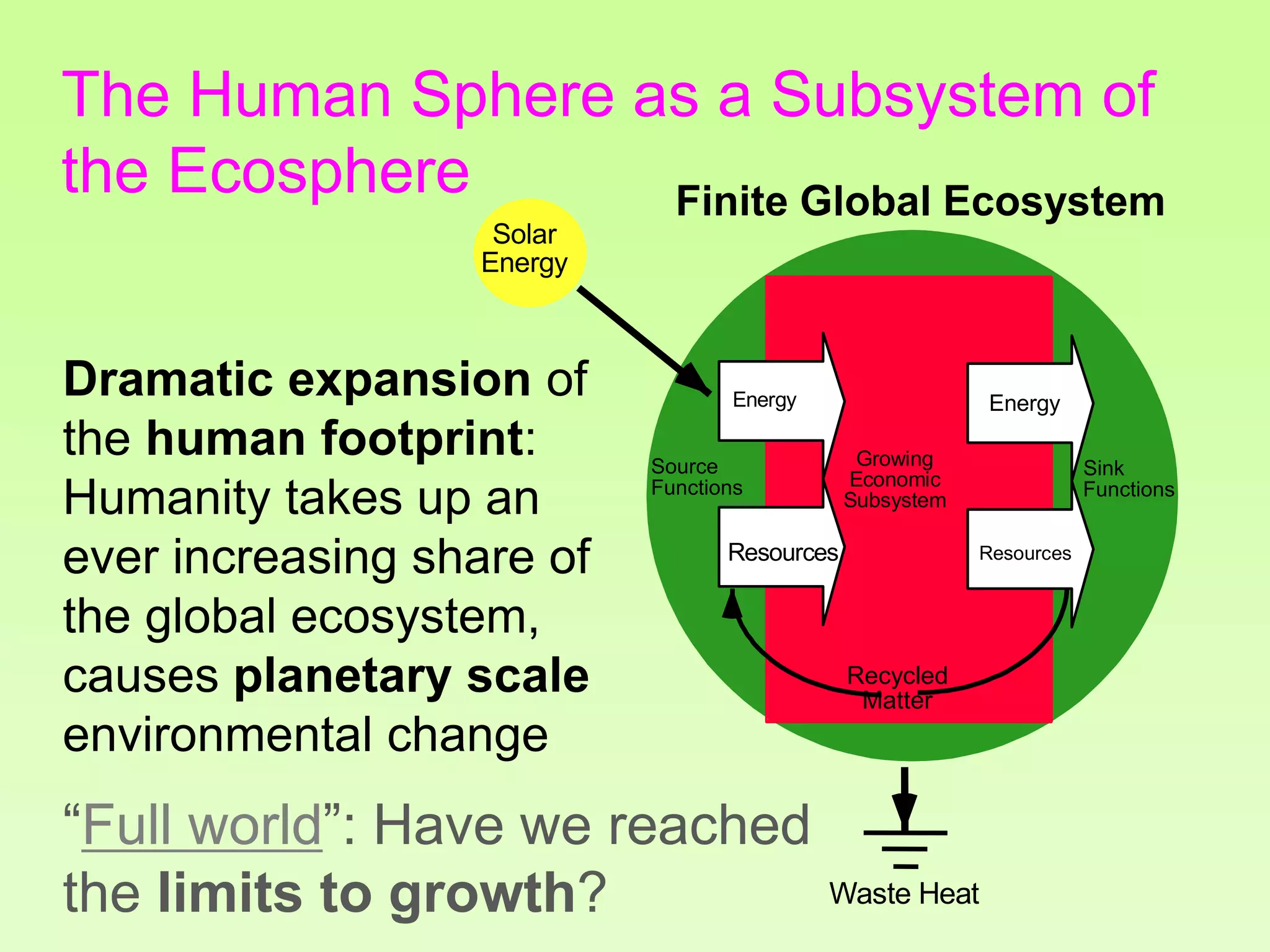
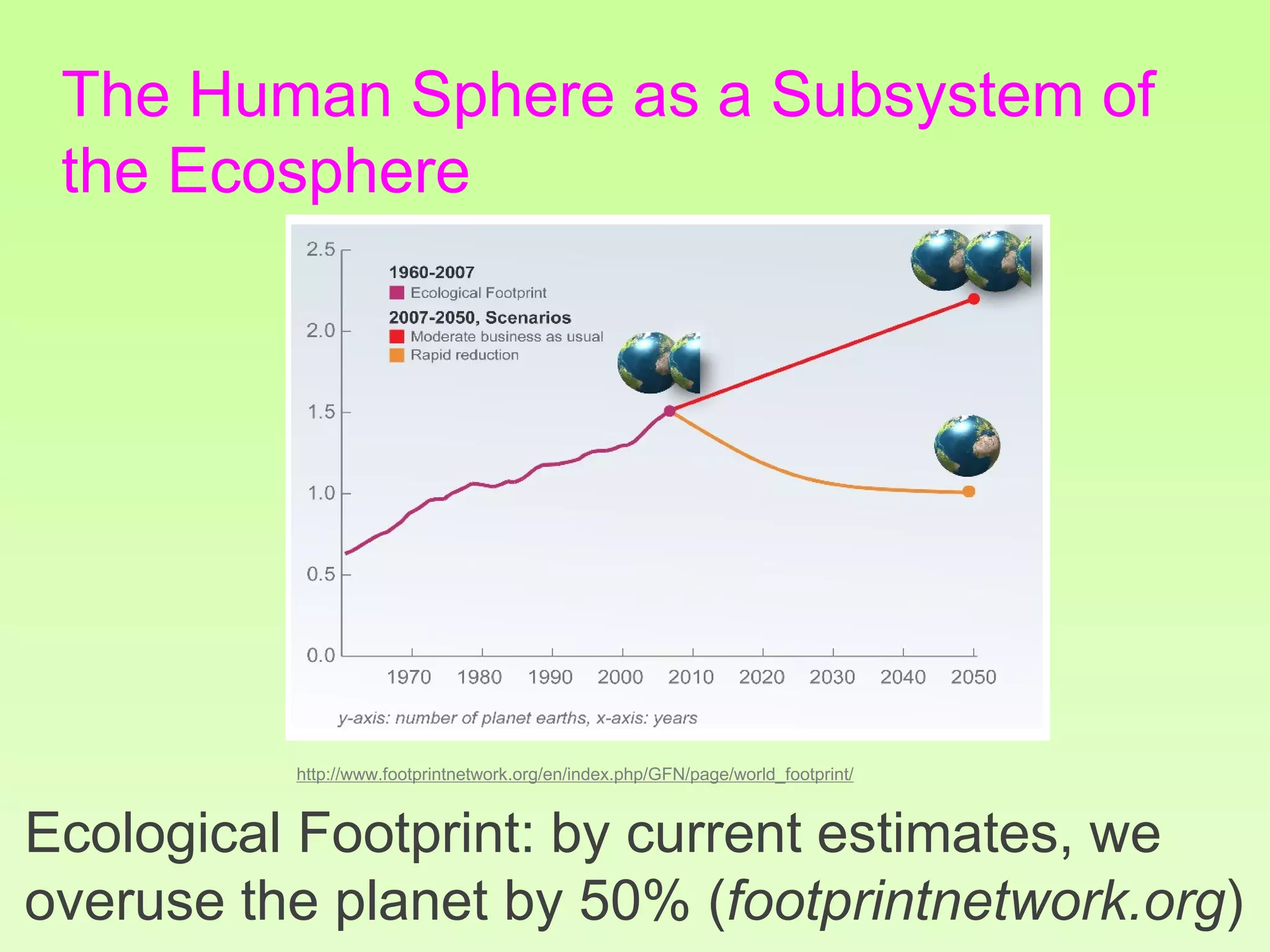
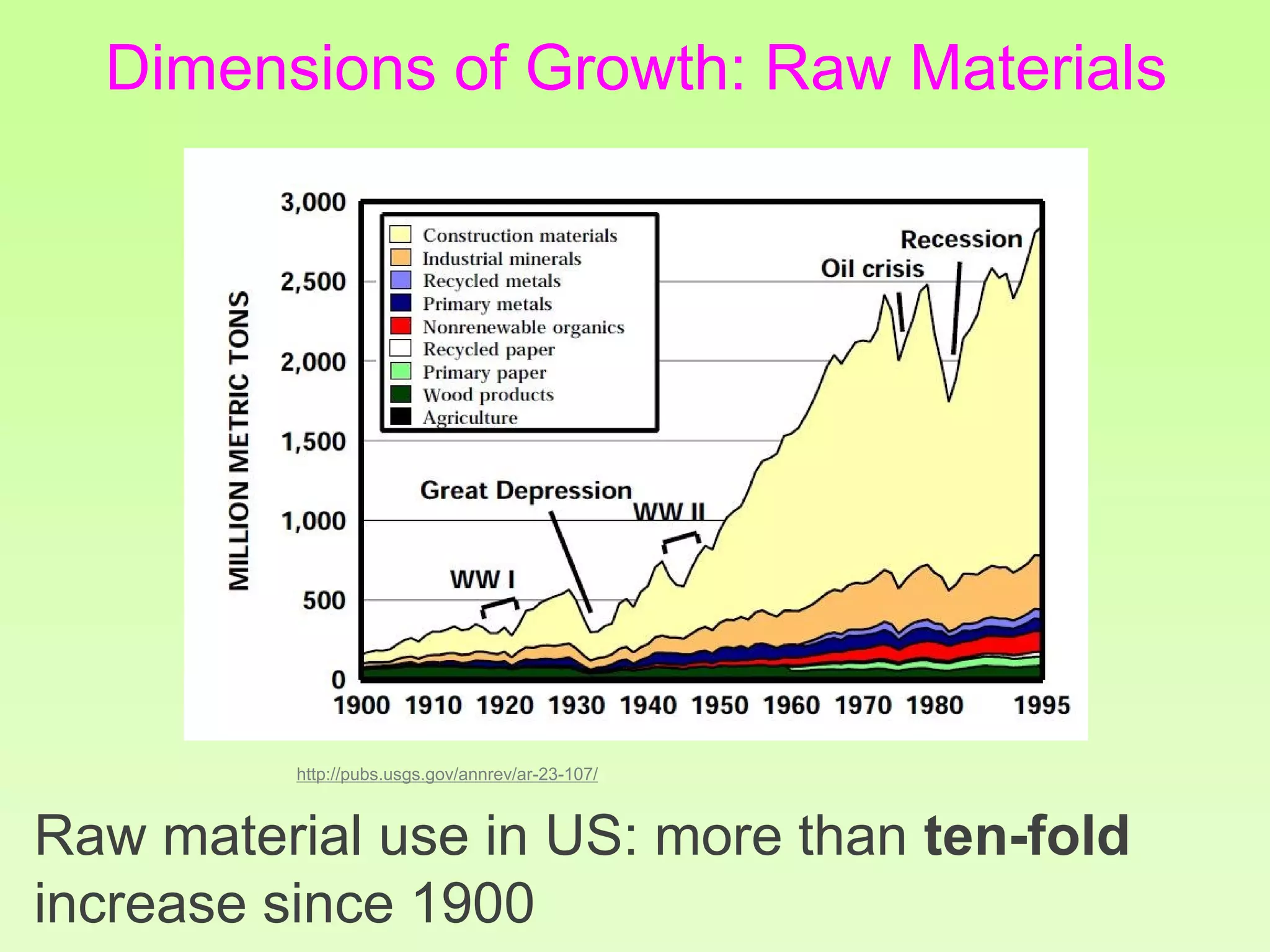
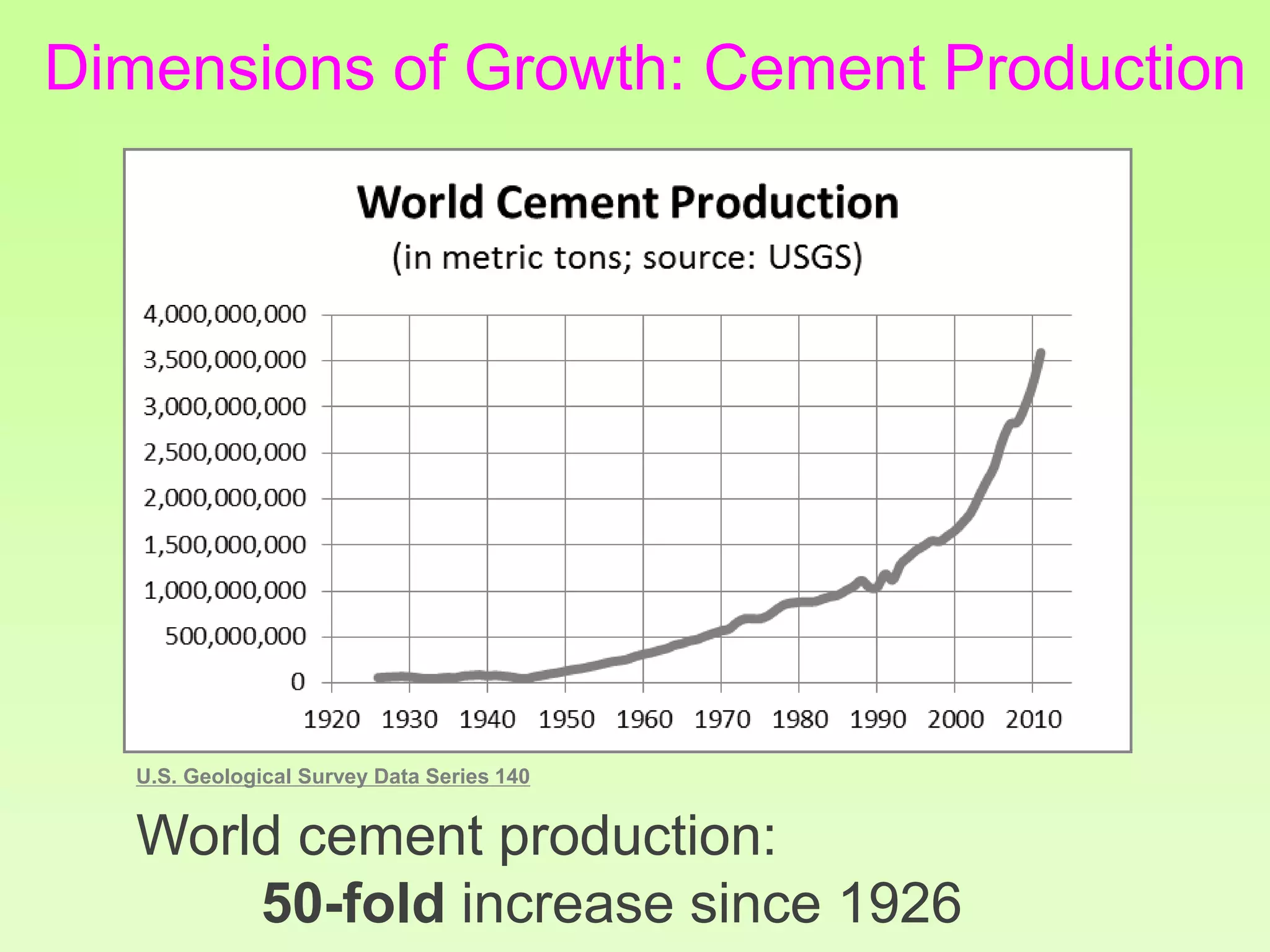
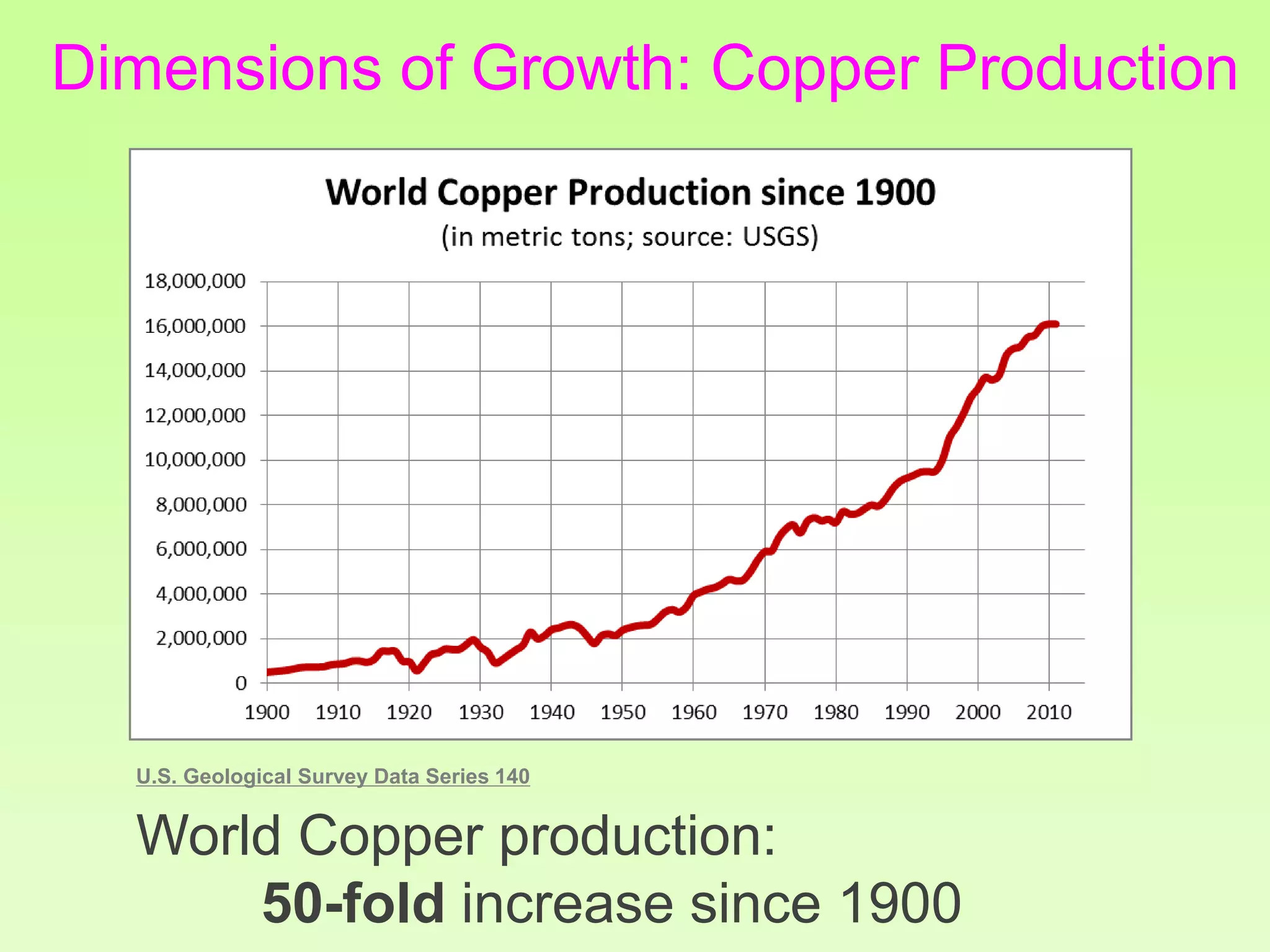
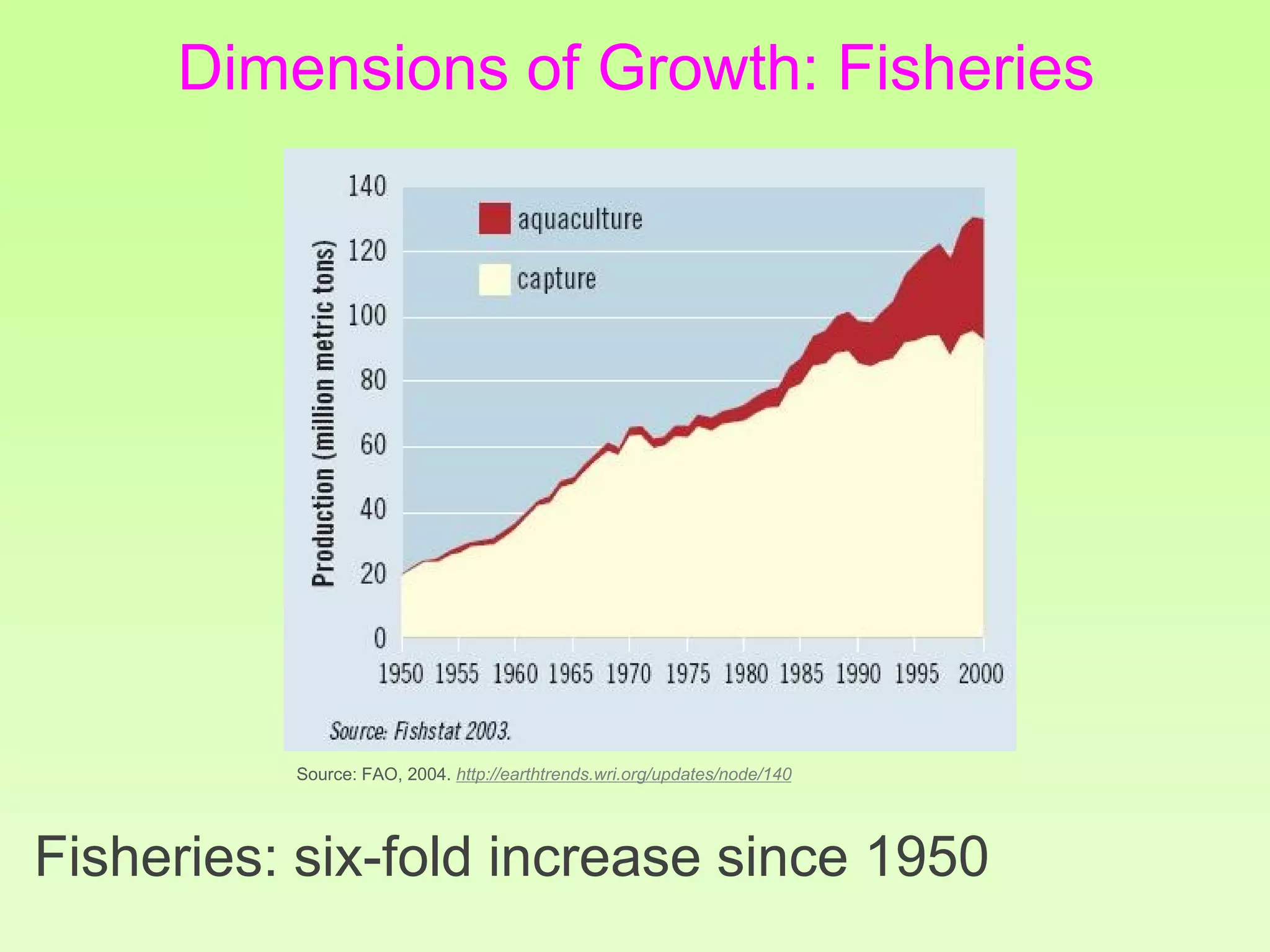
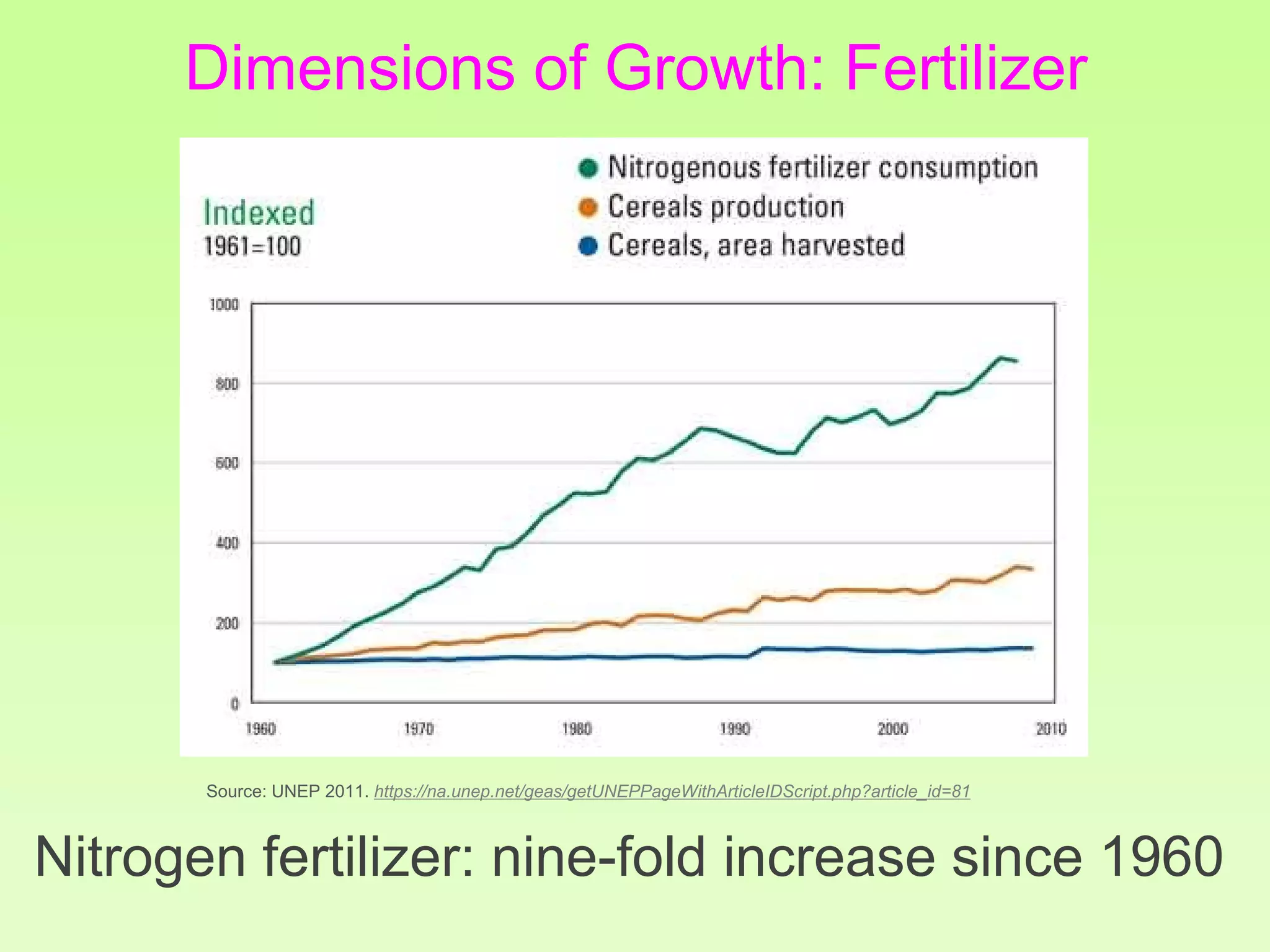
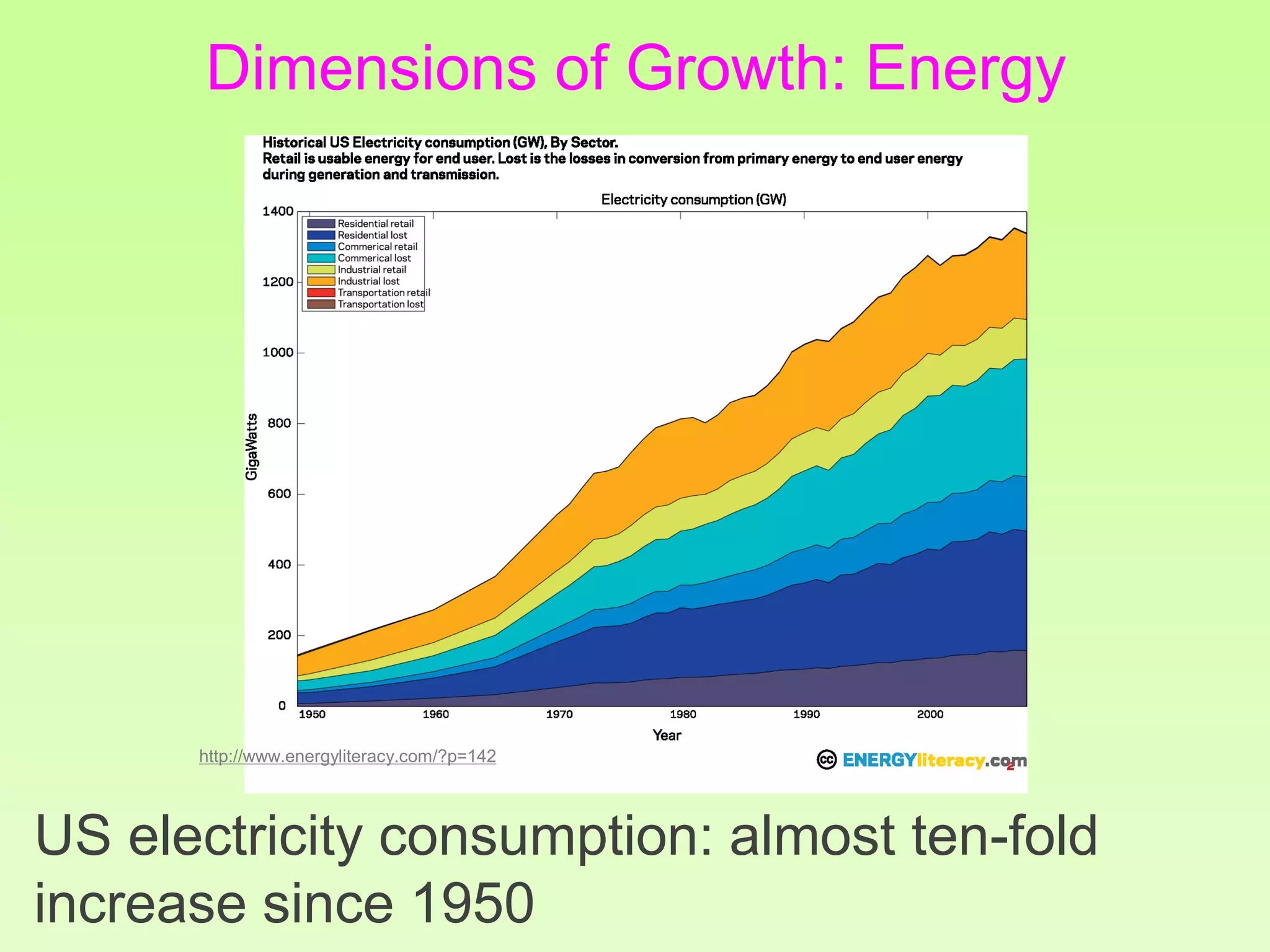
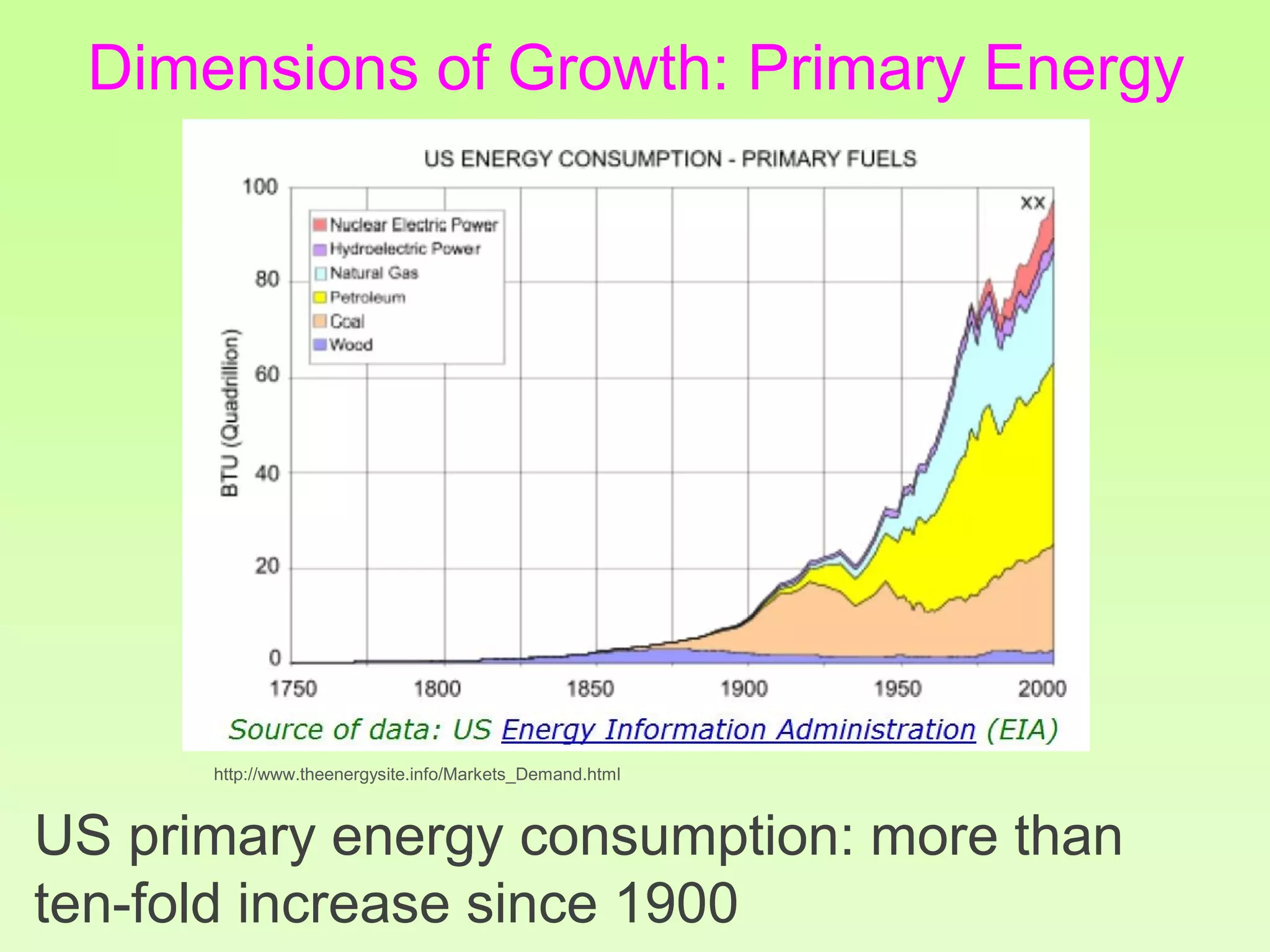
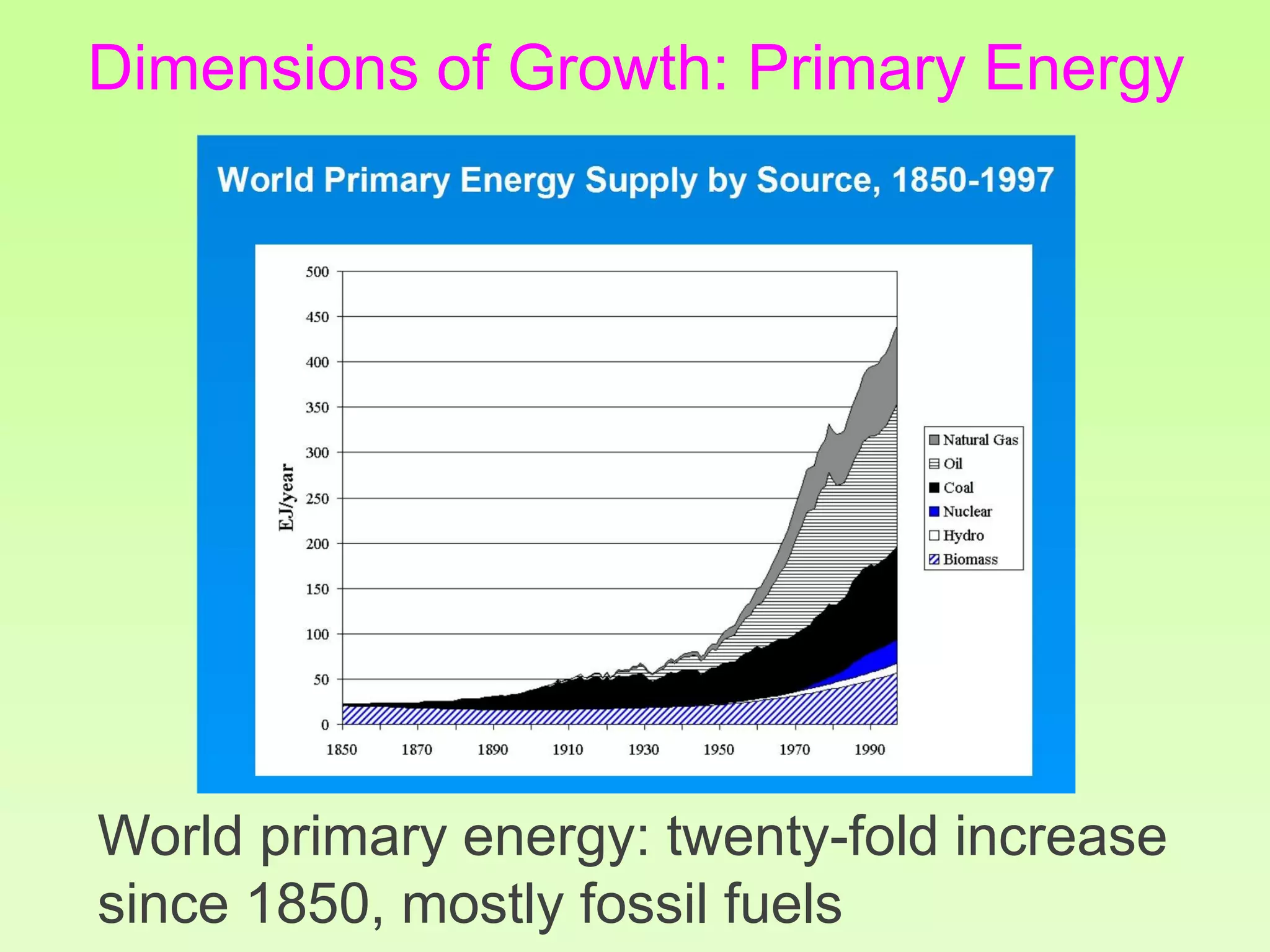
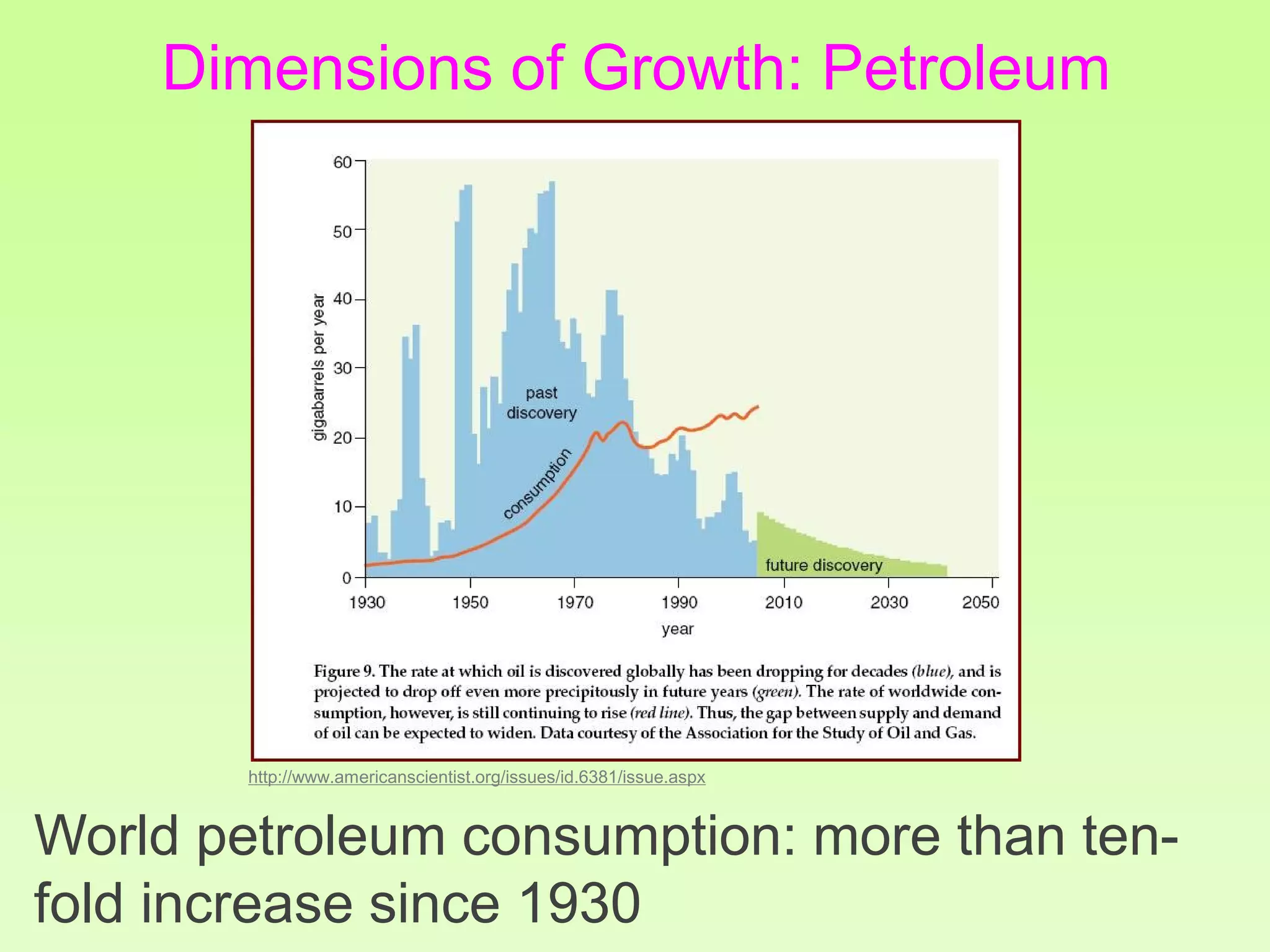
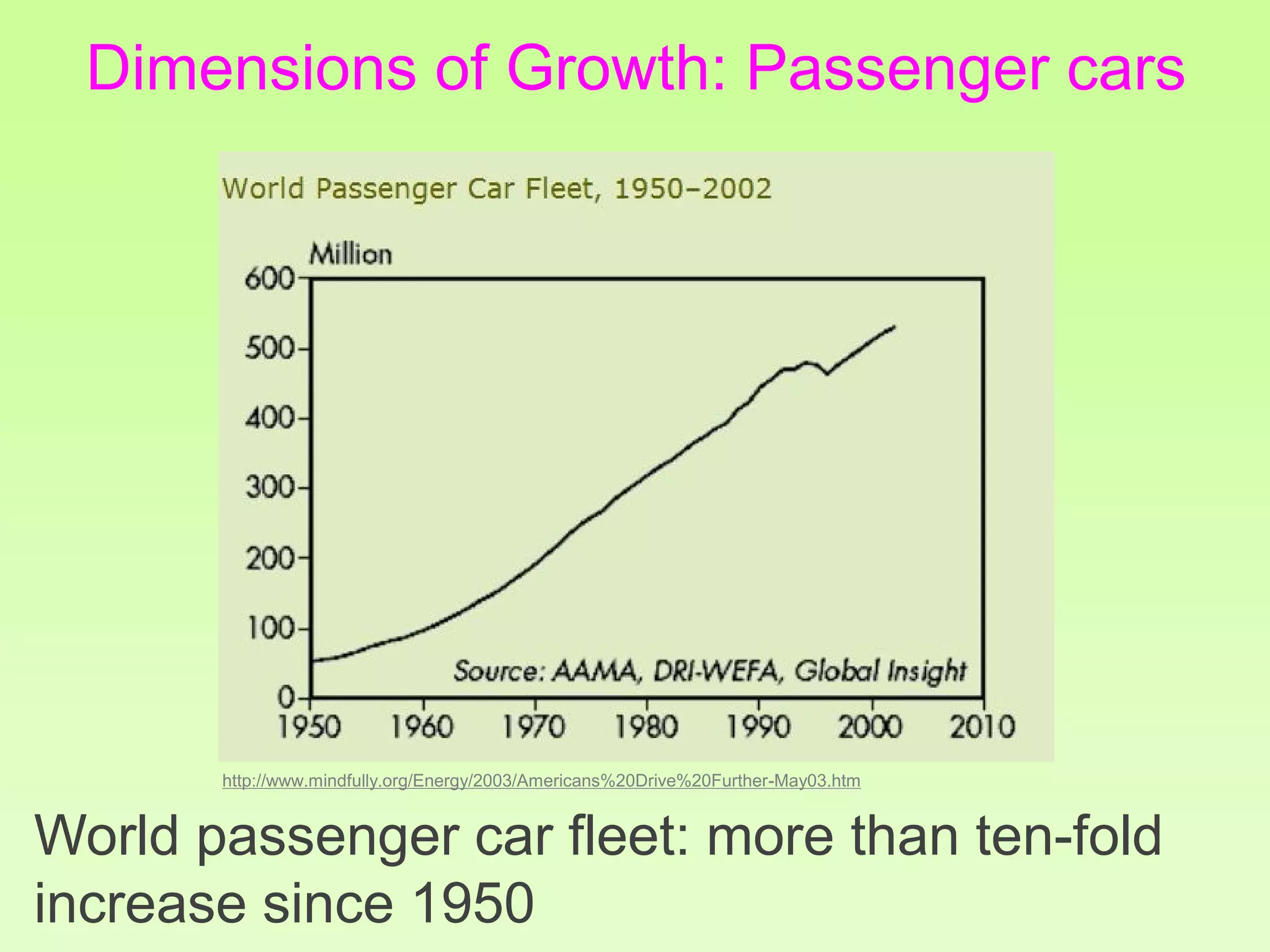
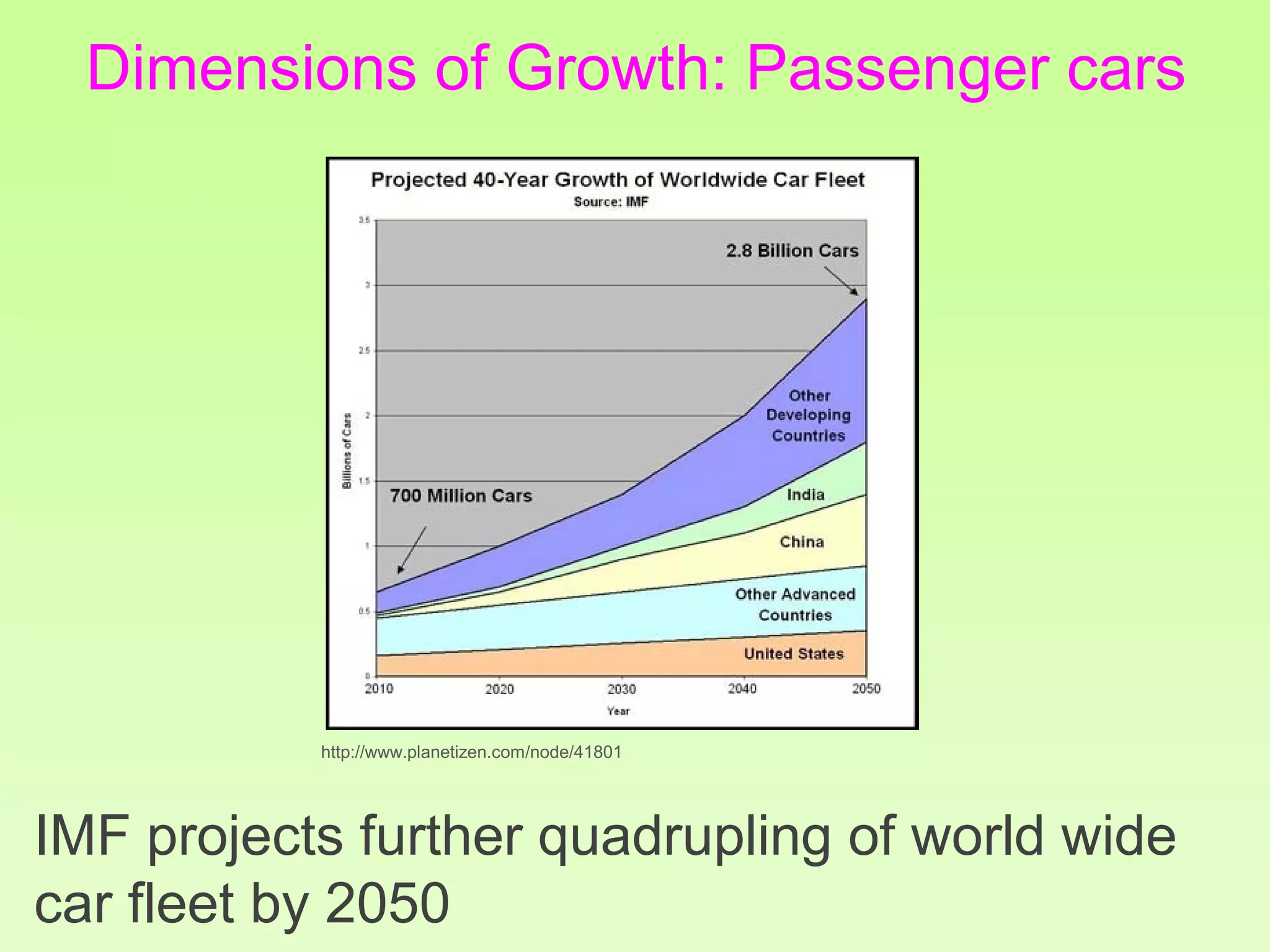
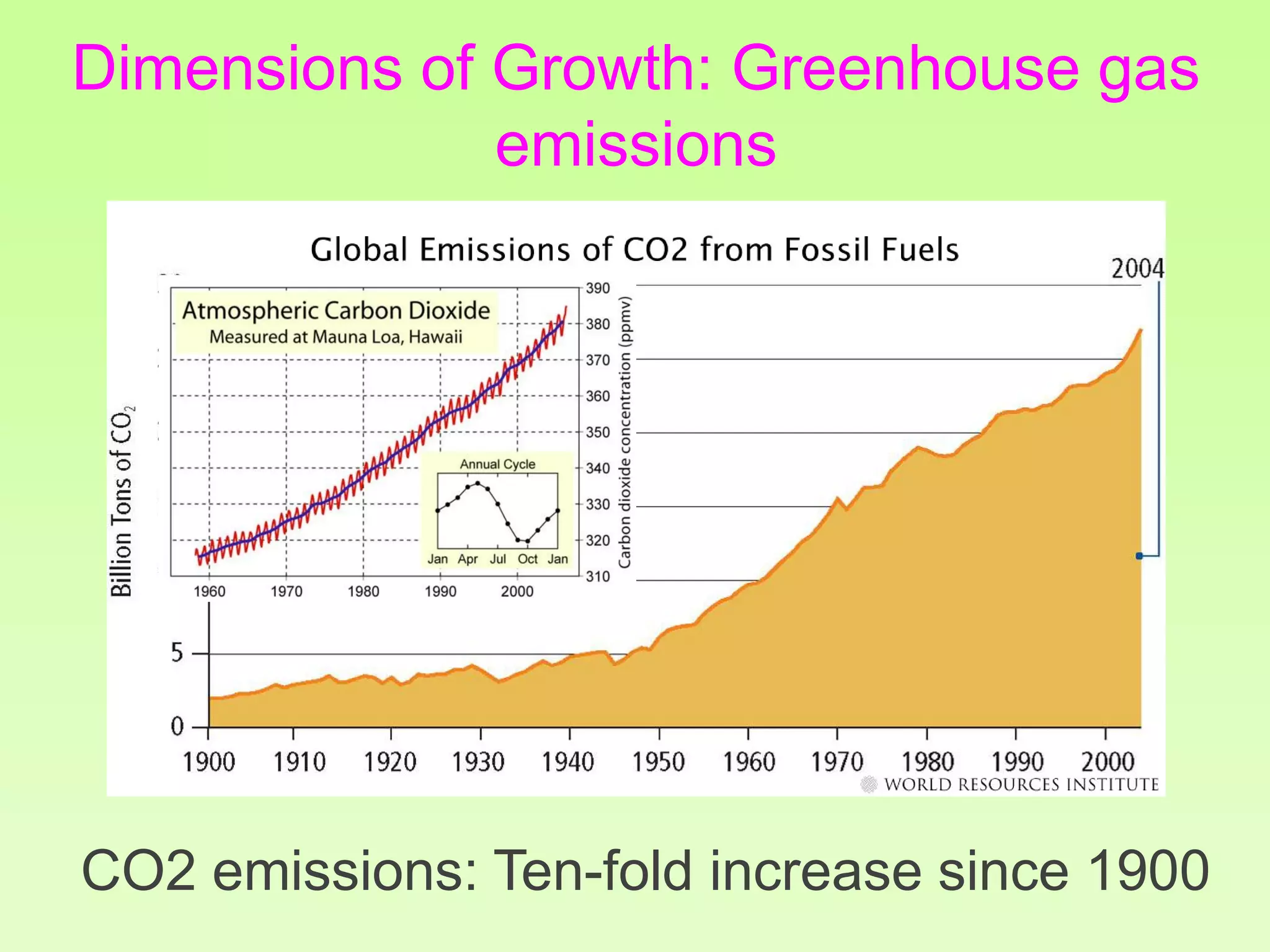
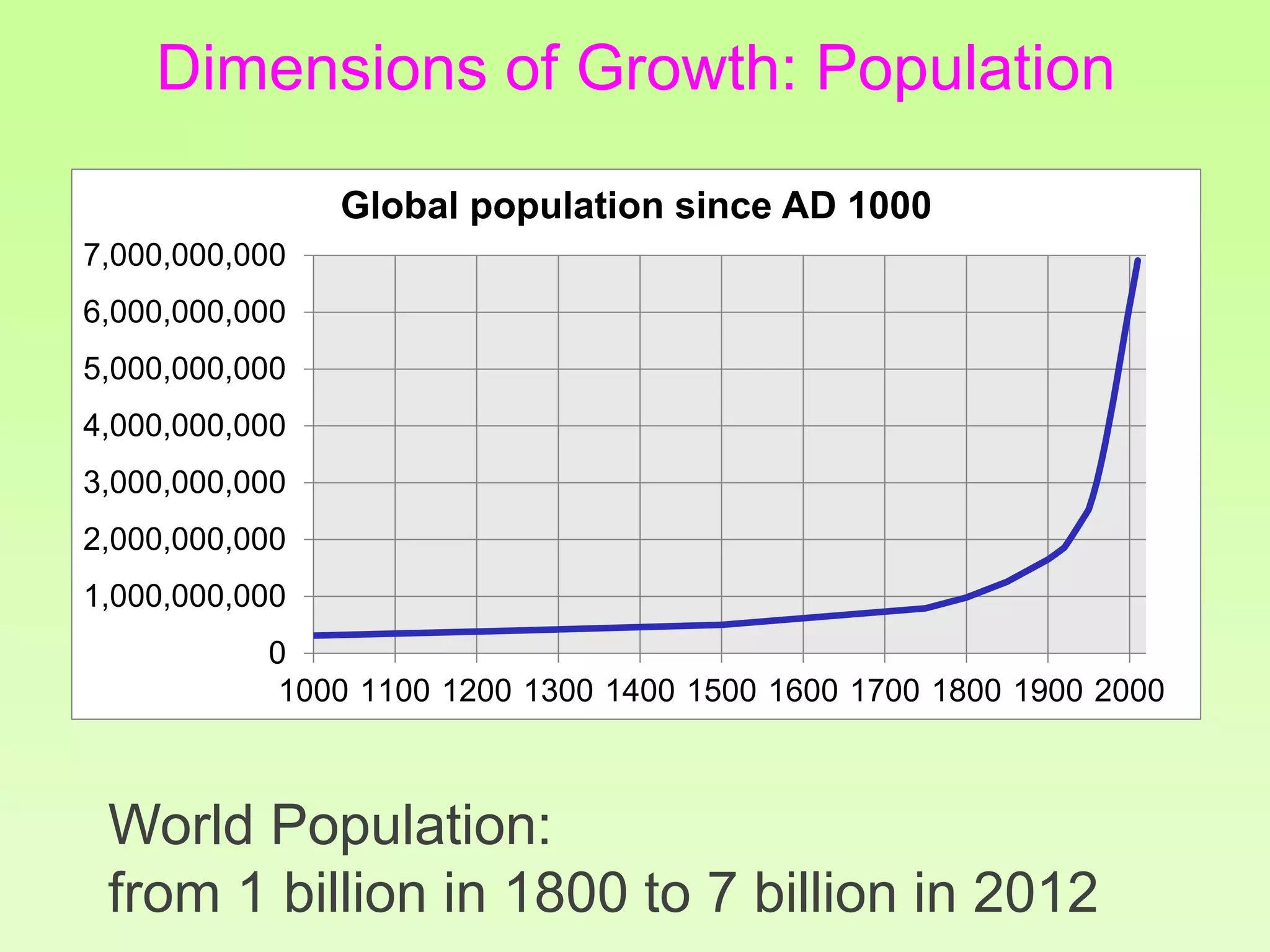
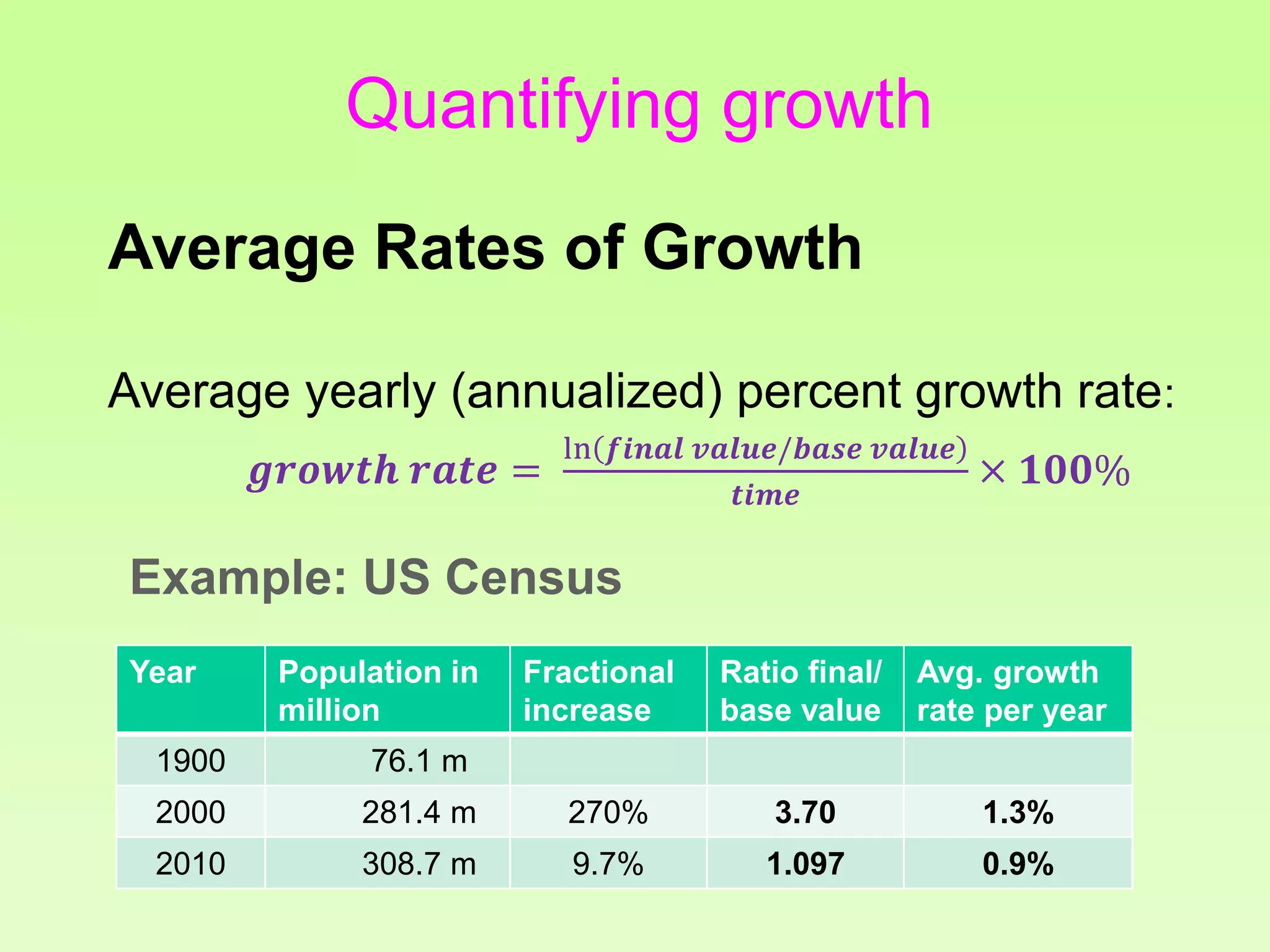
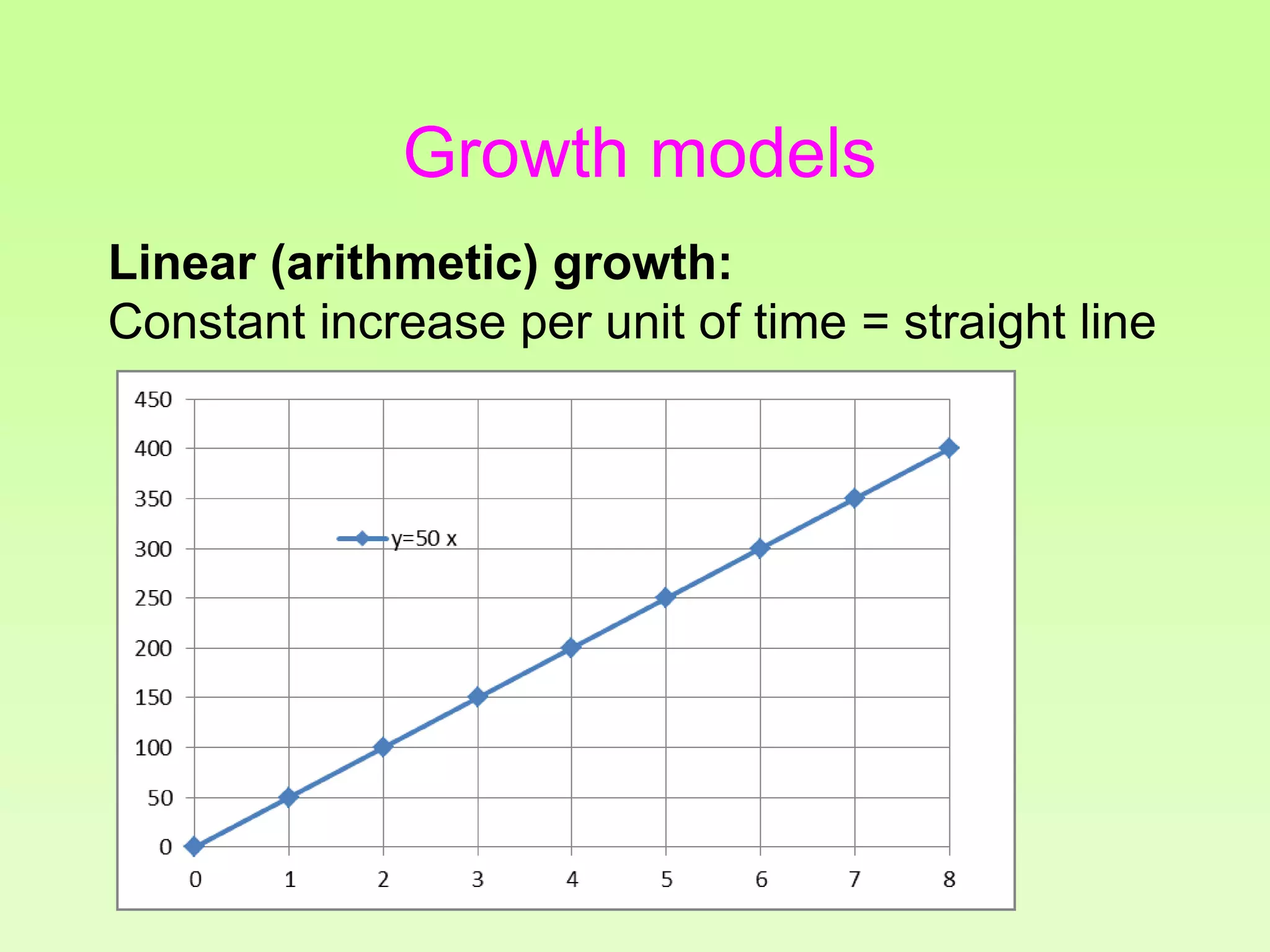
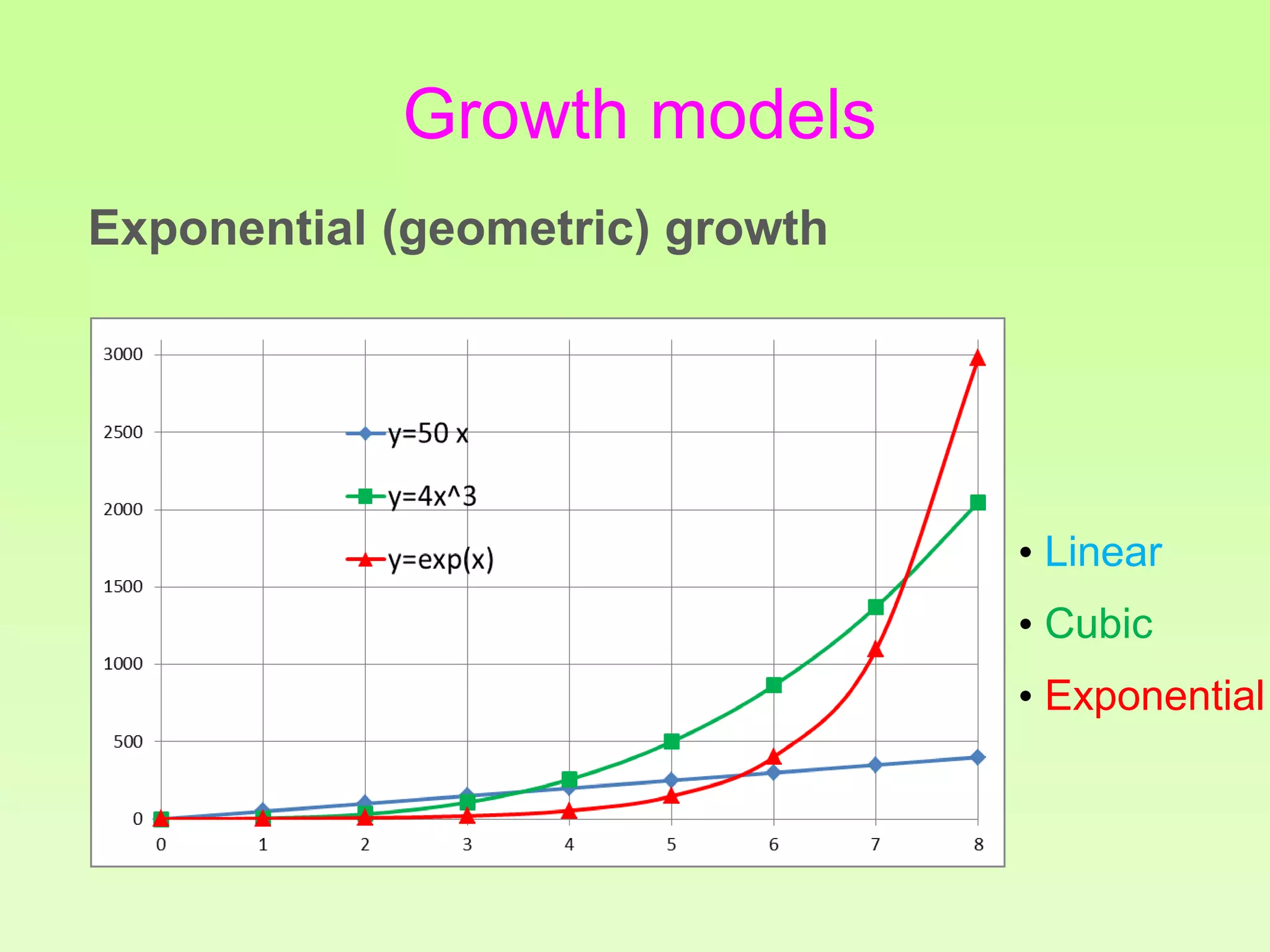
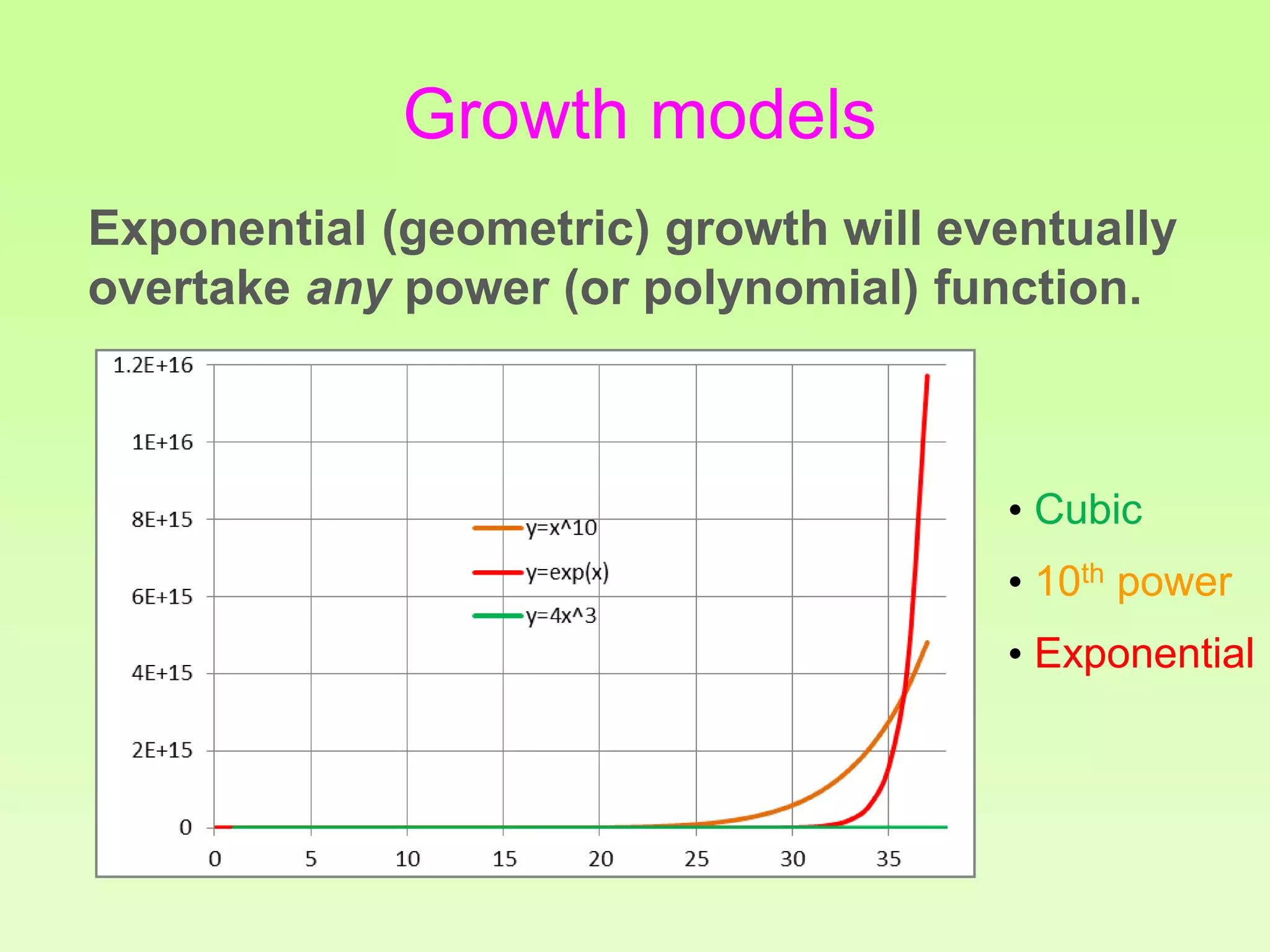
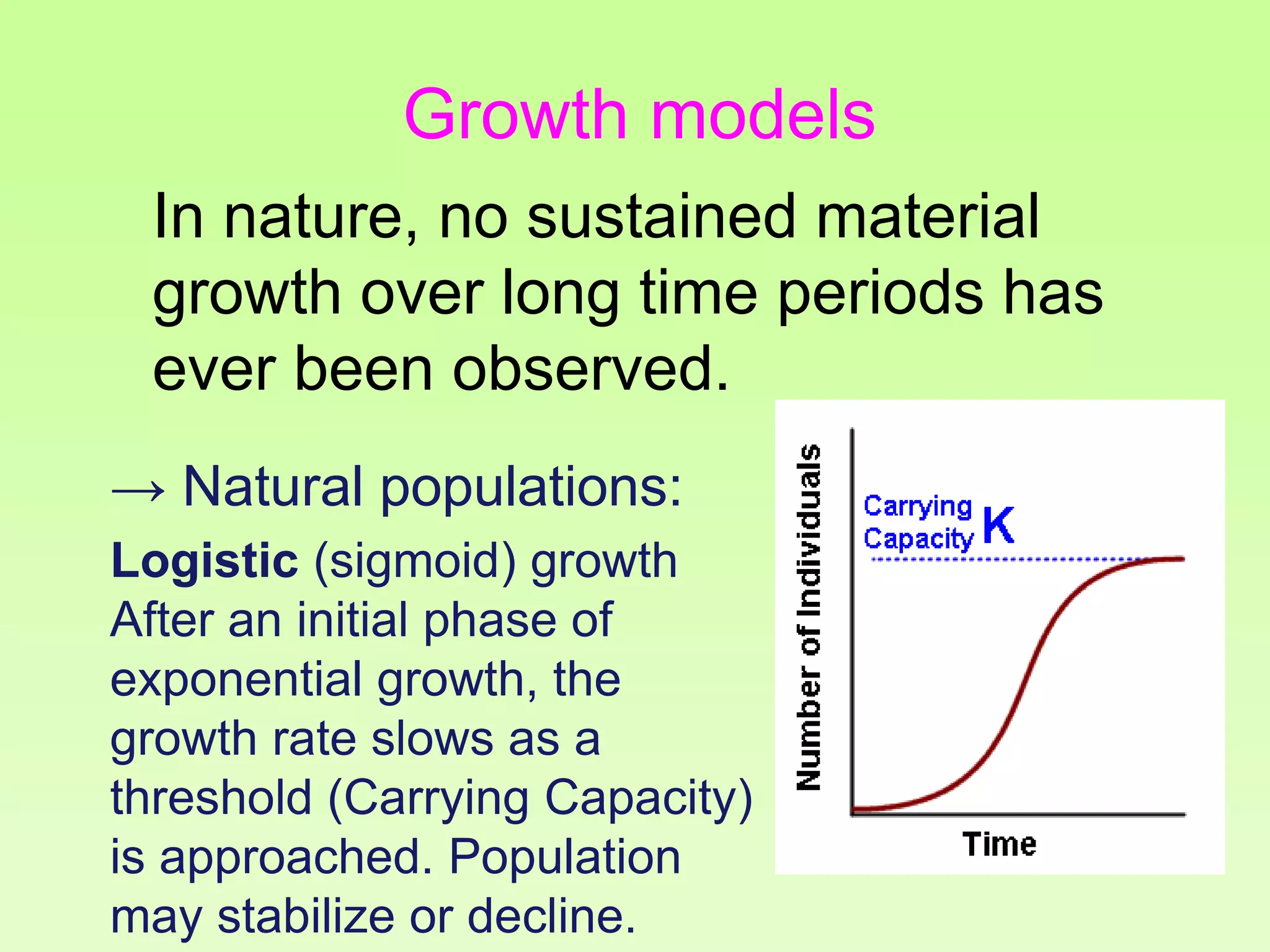
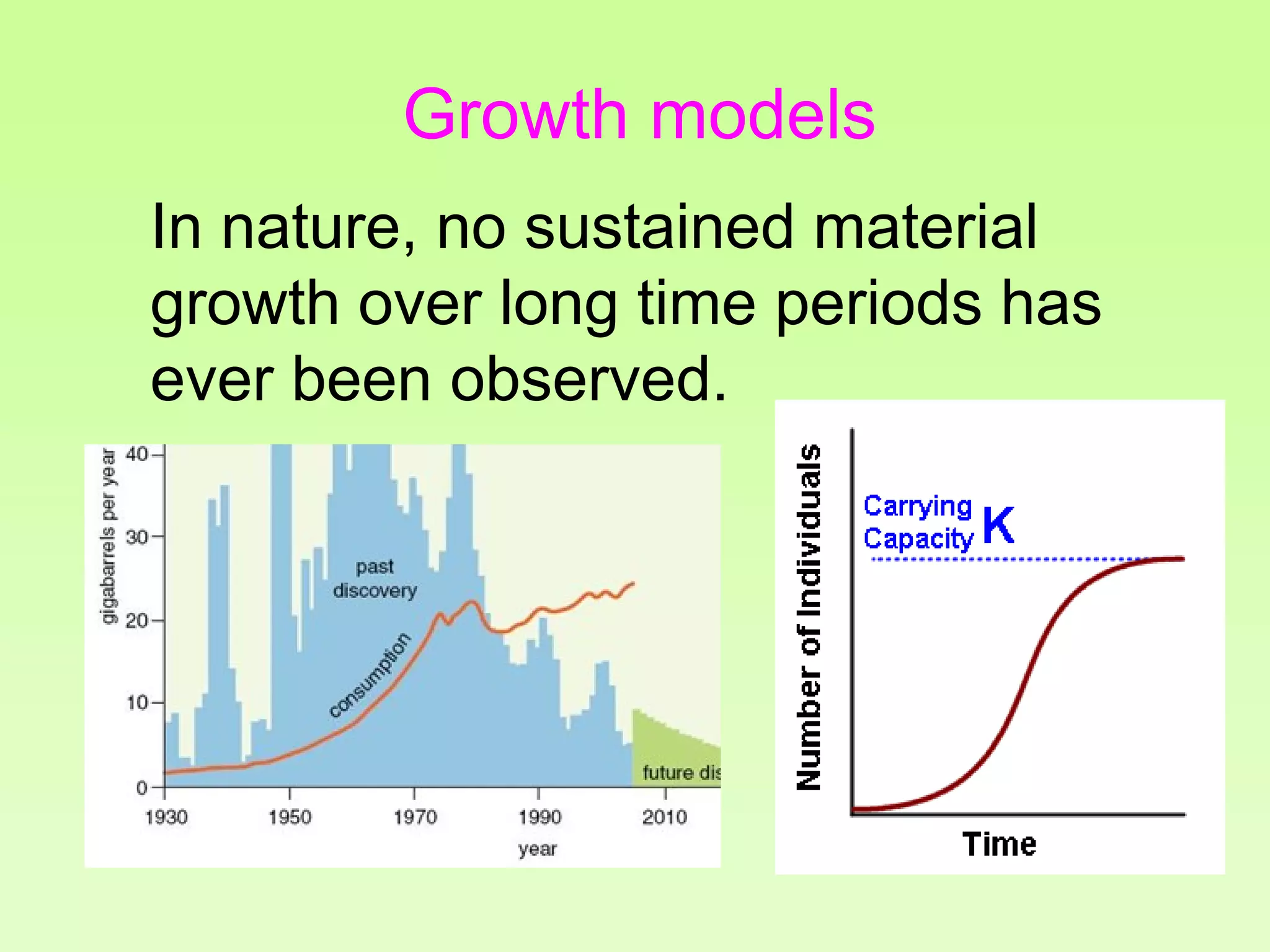
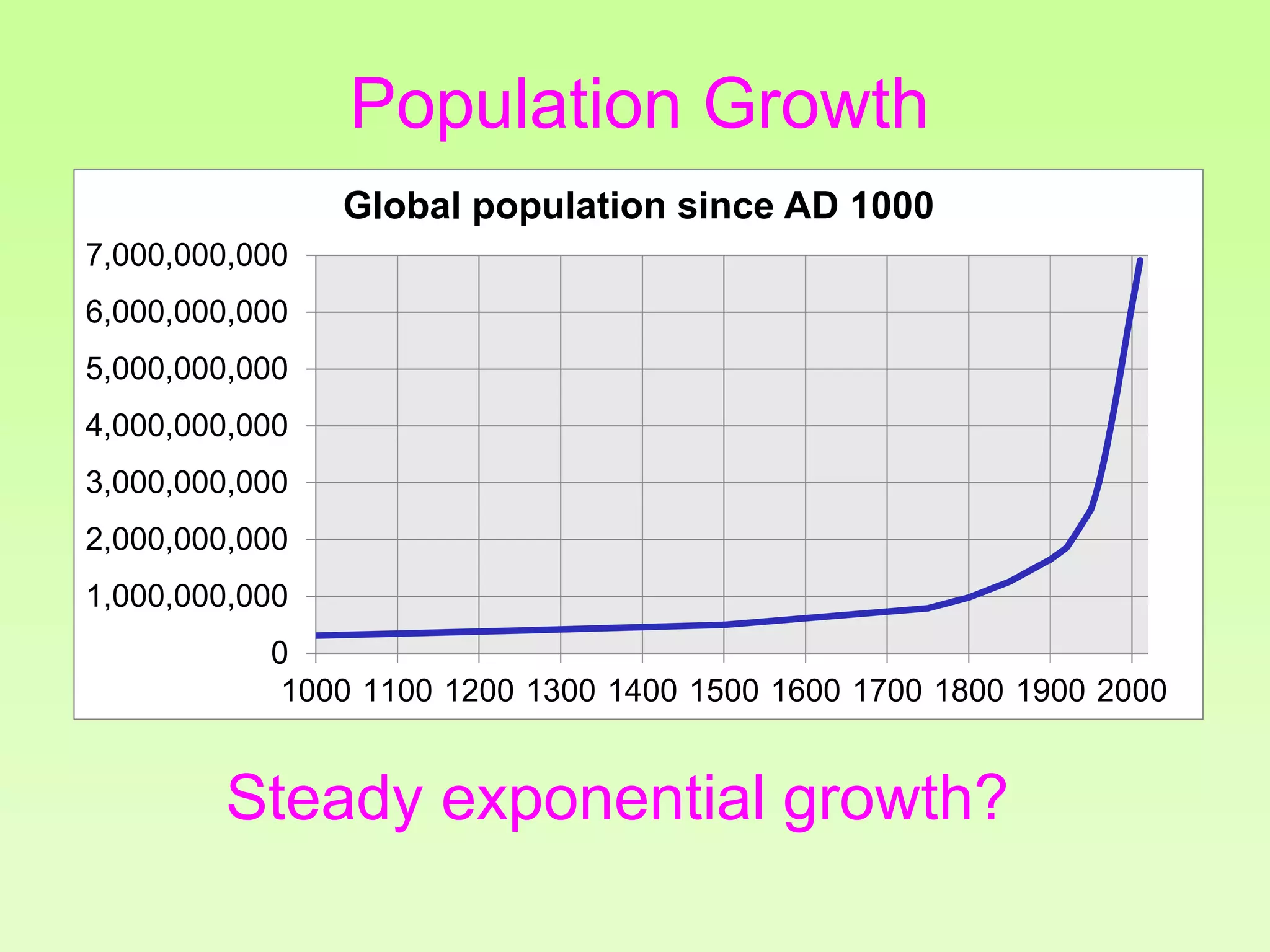
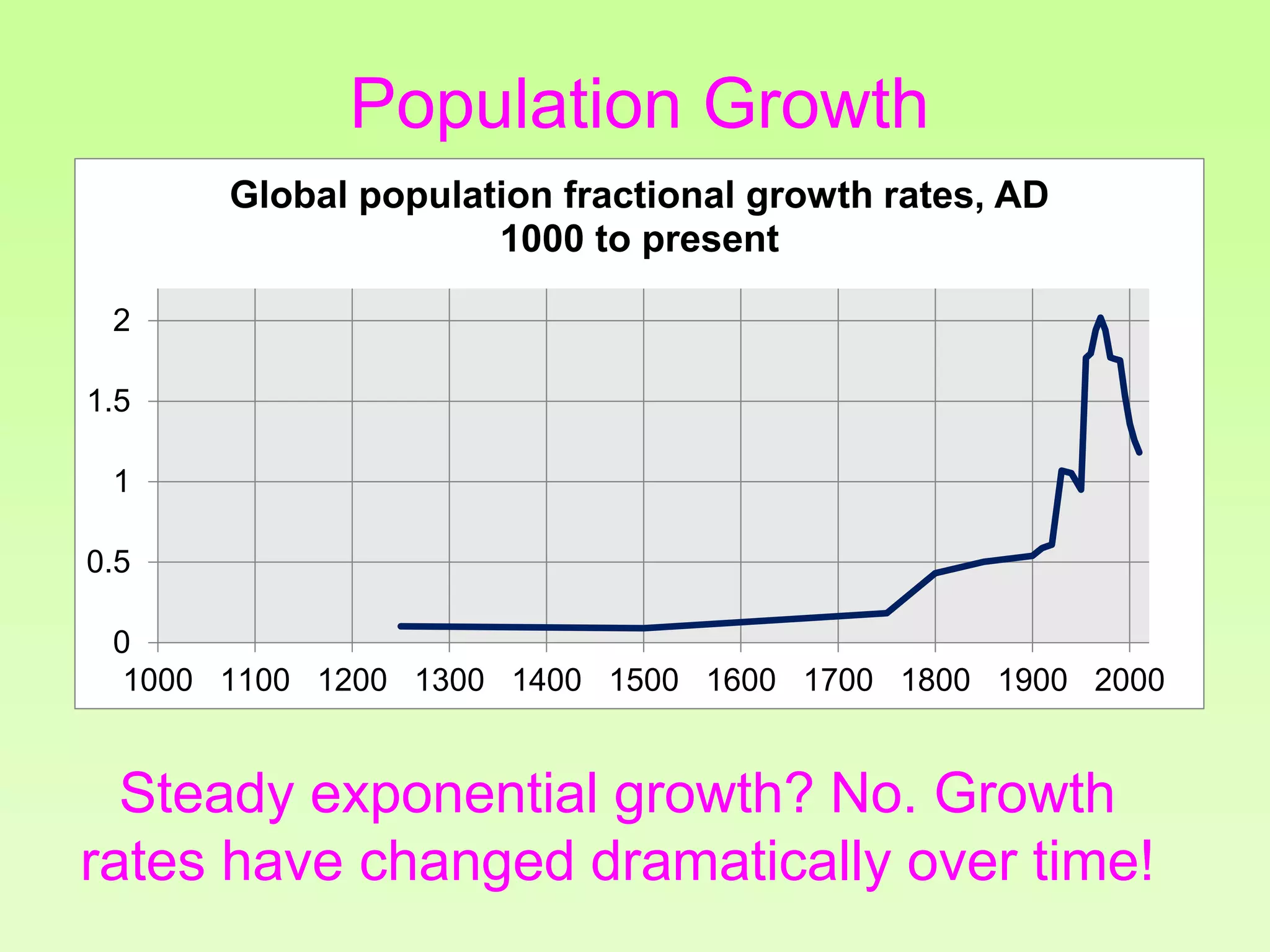
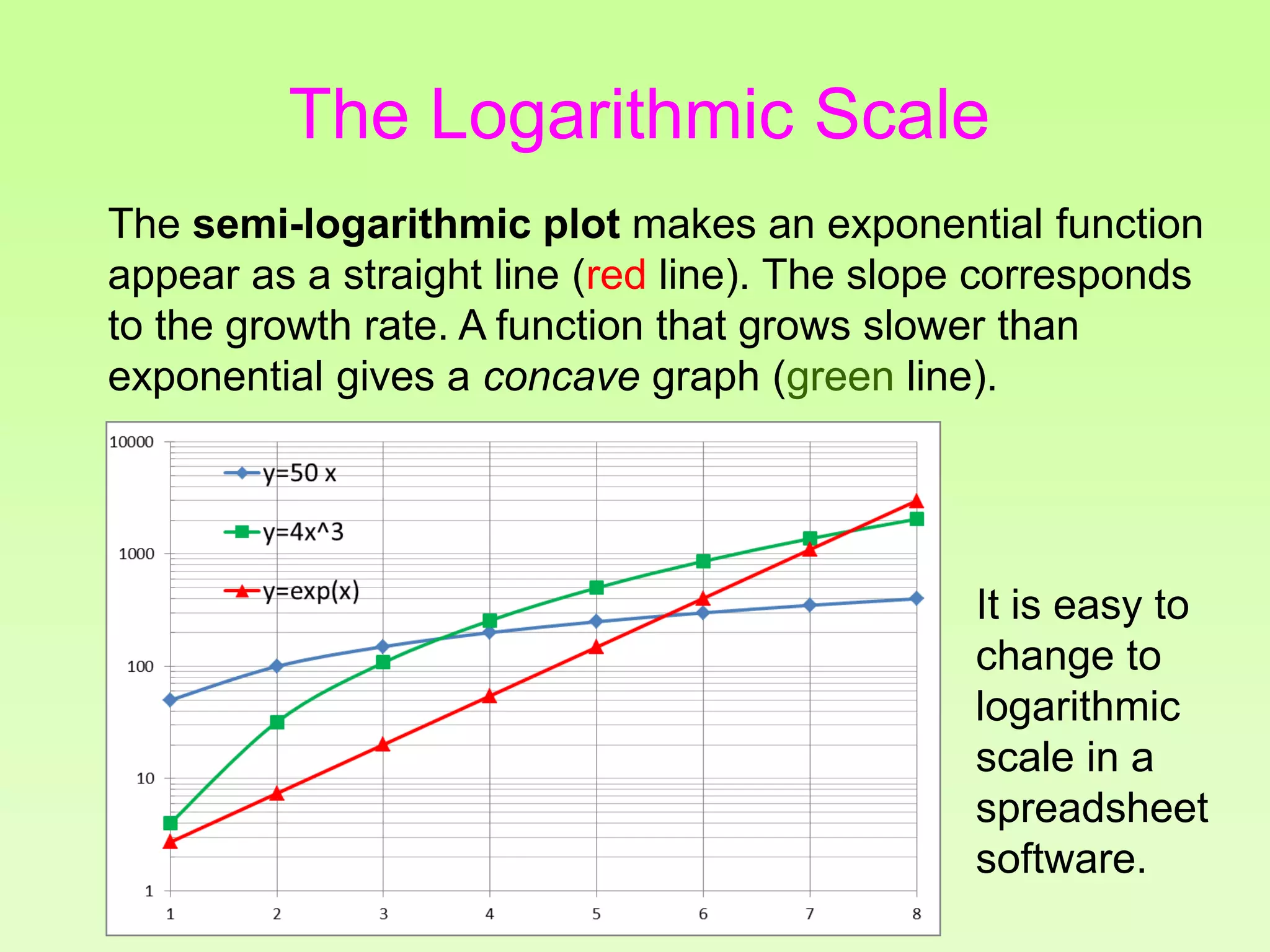
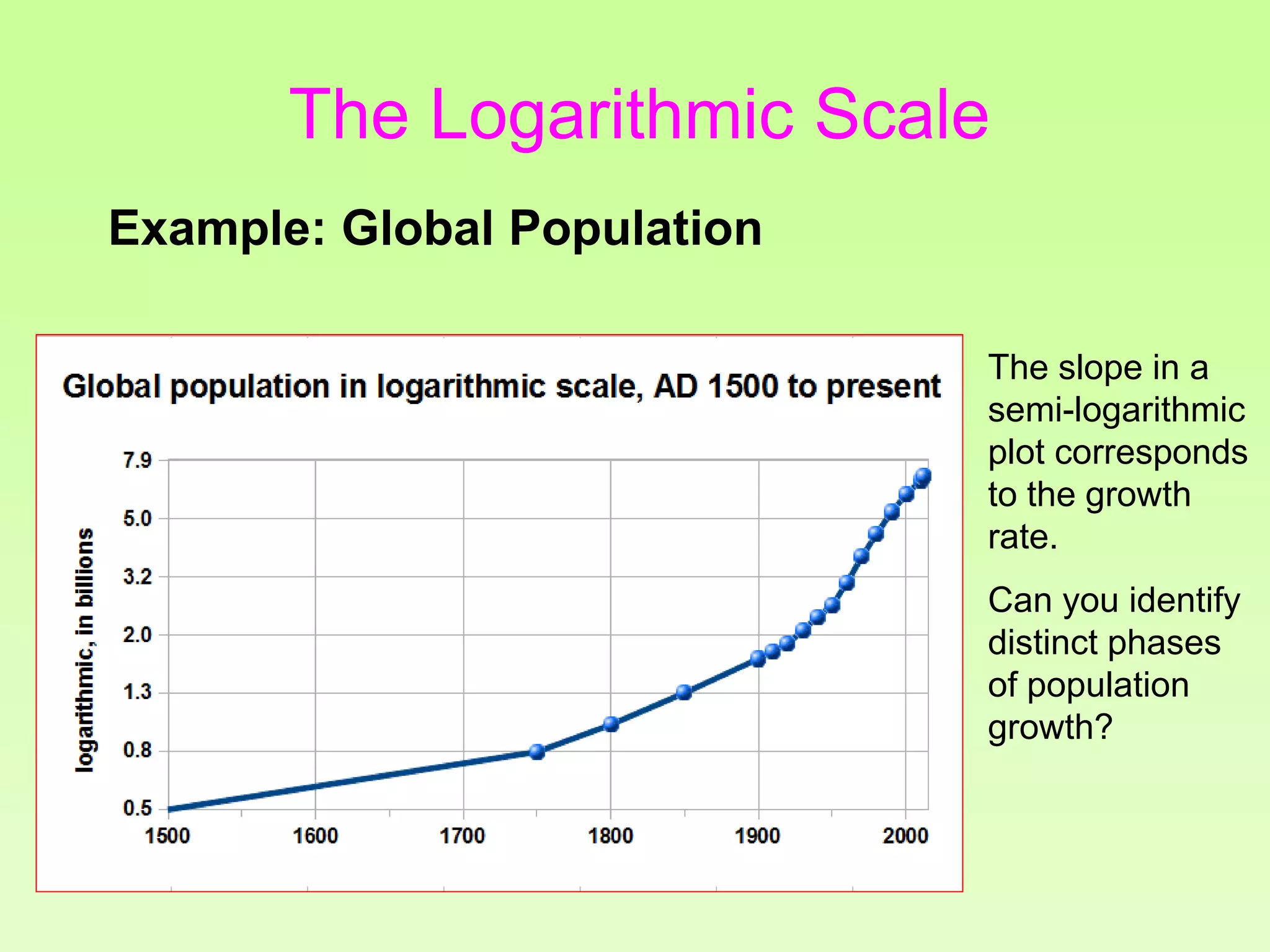
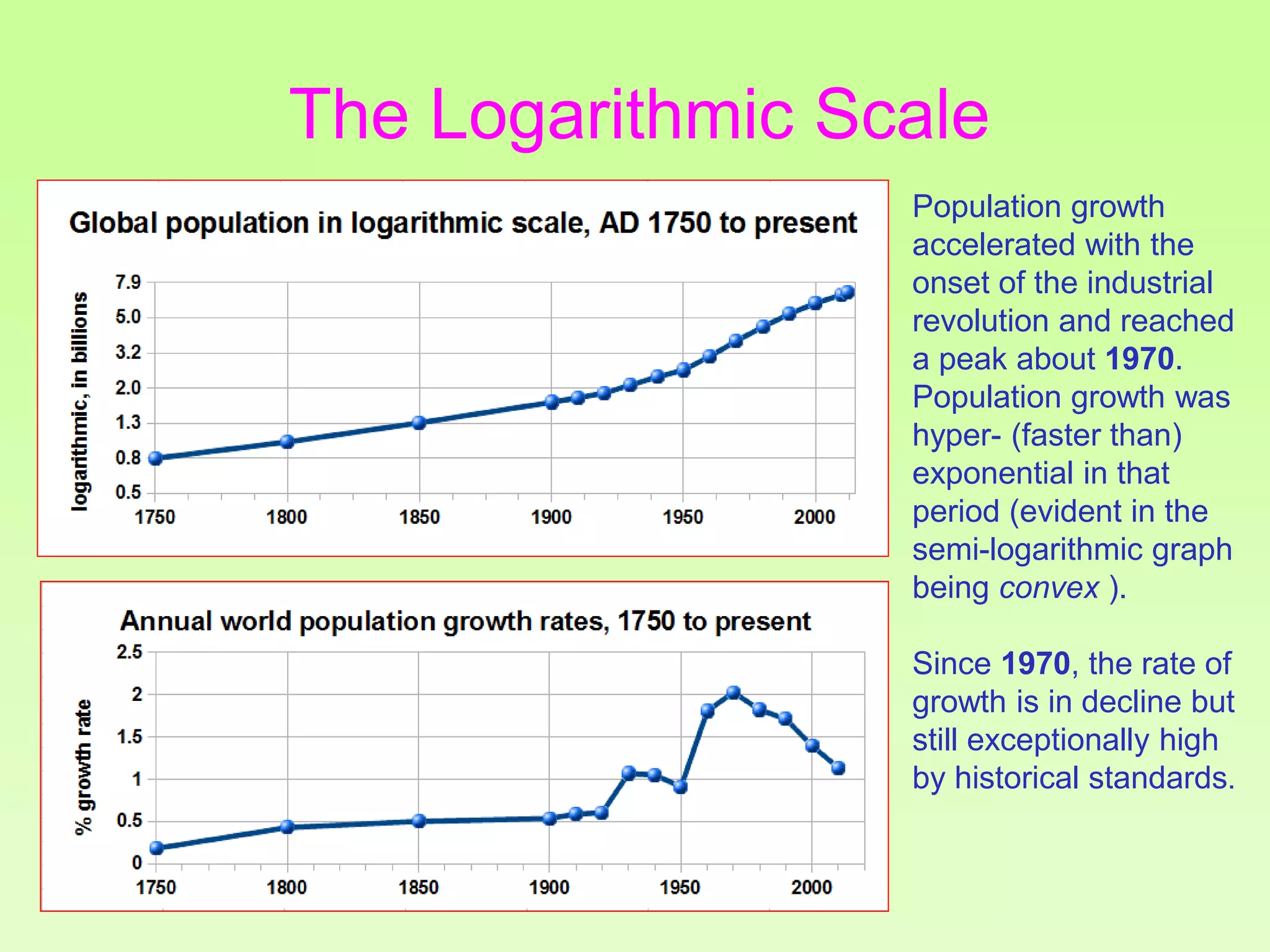
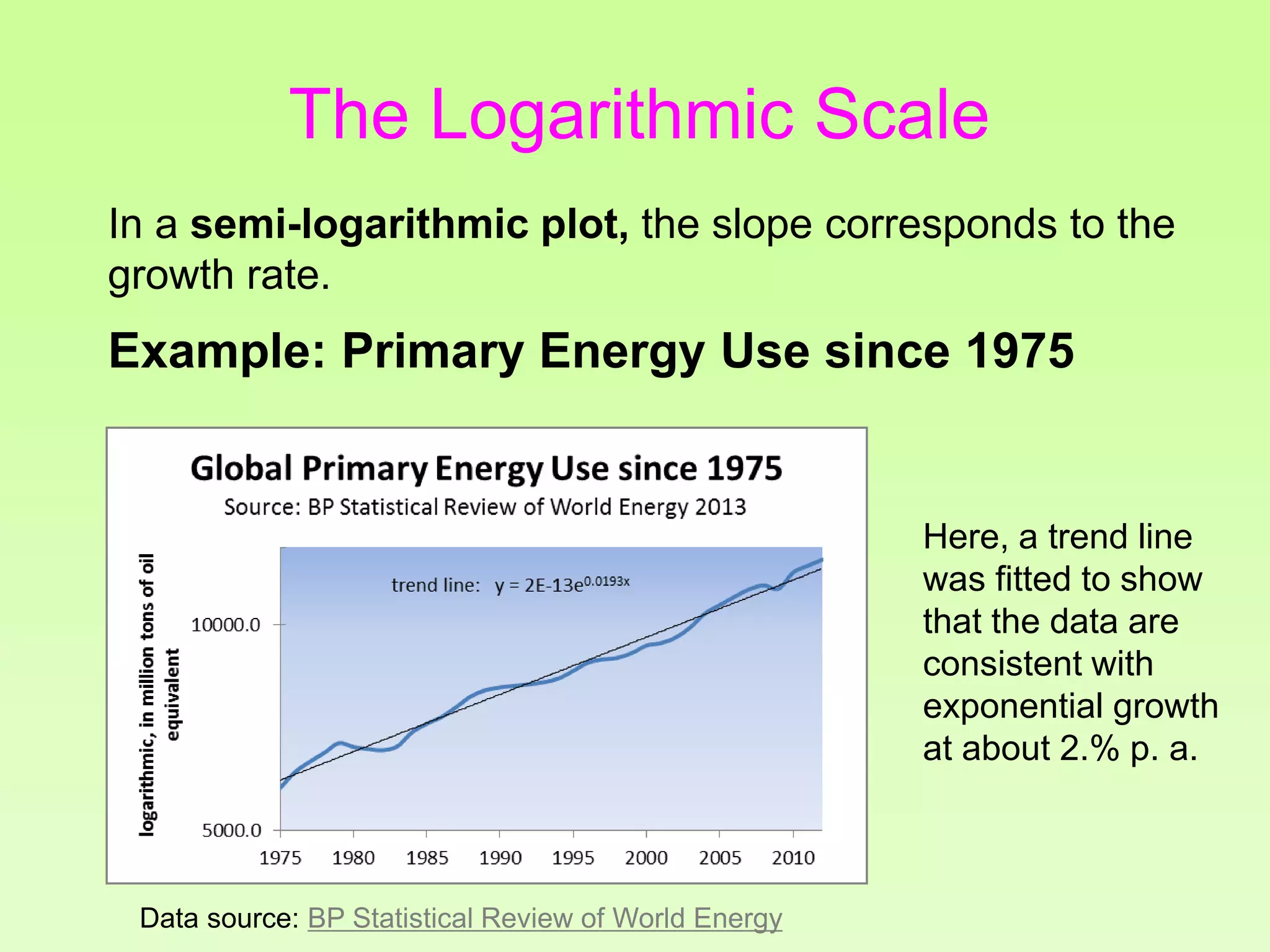
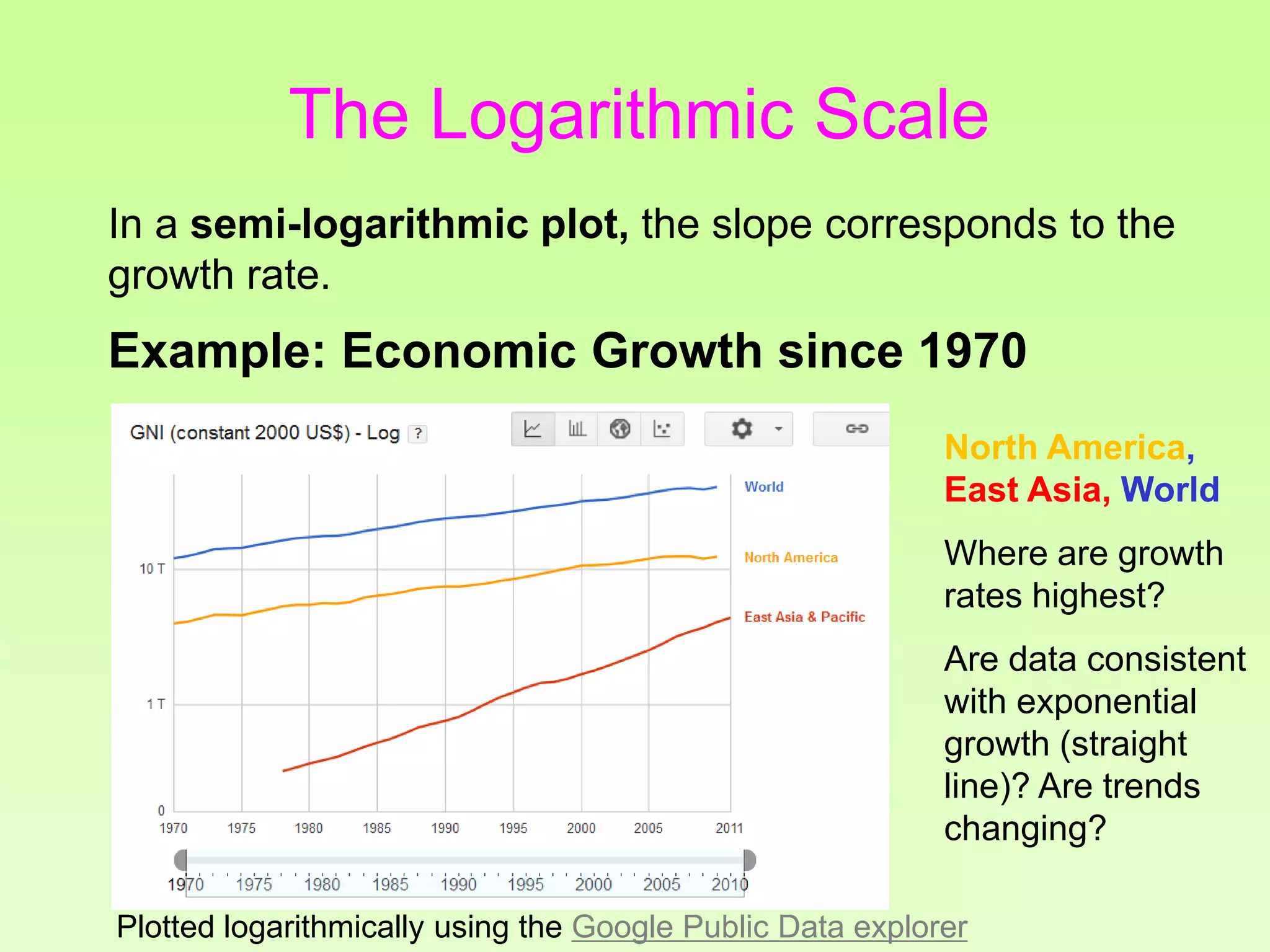
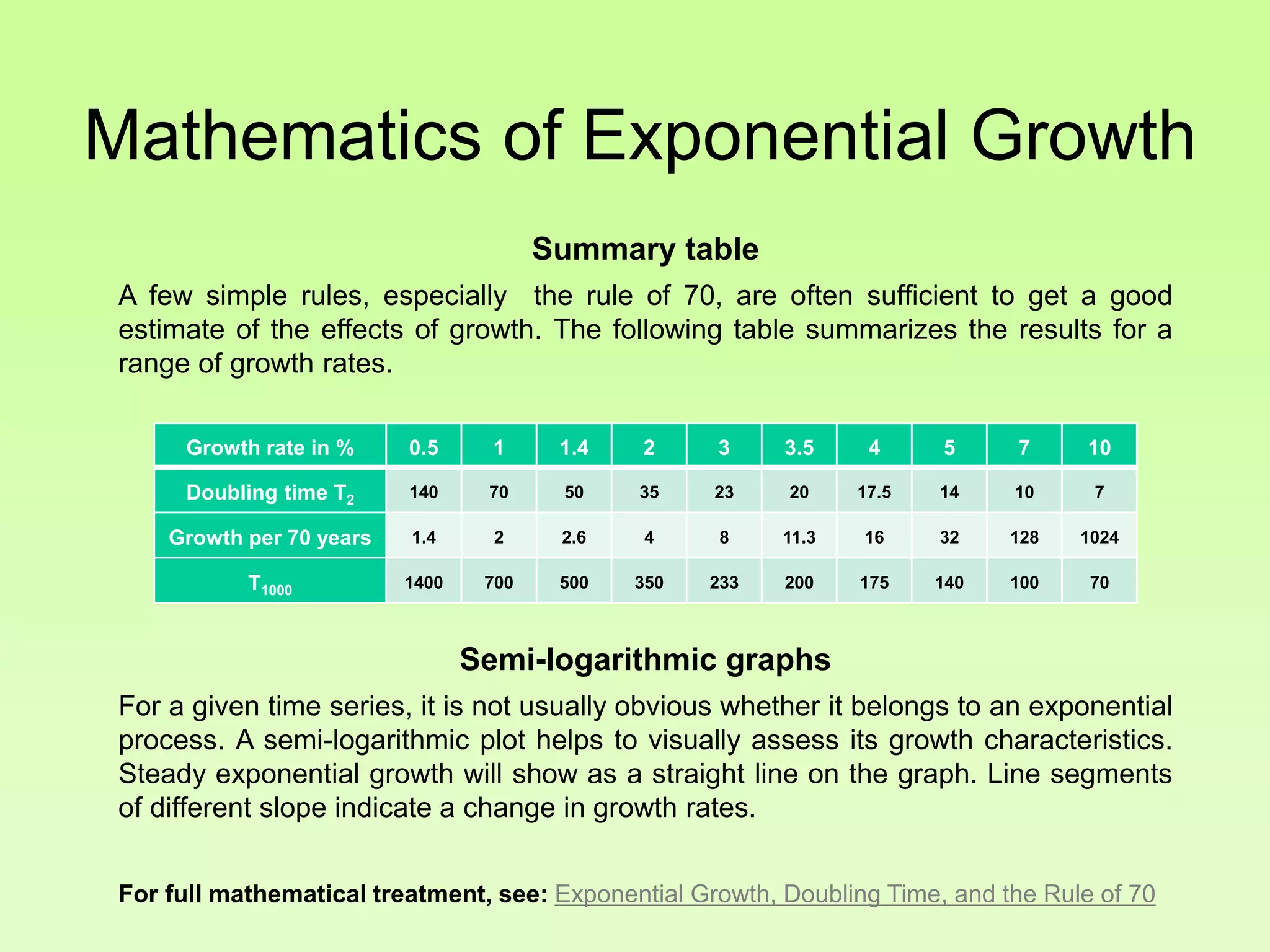
The document discusses the relationship between growth and sustainability from a systems theory perspective, emphasizing that human economic activities operate within a finite ecological ecosystem. It details the historical expansion of human impact on the environment, highlighting various growth models and quantifying methods of analysis, including absolute and relative changes. The document underlines the importance of understanding exponential growth and its implications for sustainability, warning against the continuation of unsustainable growth strategies in a 'full world'.

1. Growth in a Finite
World
Sustainability and the Exponential
Function

2. Growth in a Finite World
Sustainability and the Exponential
Function
Lecture Series in Sustainability
Science
by
Toni Menninger MSc
http://www.slideshare.net/amenning/
toni.menninger@gmail.com

3. Growth in a Finite World
1. Growth and Sustainability: A systems theory perspective
The Human sphere as a subsystem of the ecosphere
2. Dimensions of Growth – a historical perspective
3. Quantifying Growth
• Actual (absolute) change
• Fractional (relative) change
• Average rates of growth
4. Growth Models
• Linear growth
• Exponential growth
• Logistic growth

4. Growth in a Finite World
5. Exponential Growth
• Doubling Time
• Rule of 70
• The power of the powers of 2
• The Logarithmic Plot
6. Summary
7. Further Readings
8. Appendix: The Mathematics of Exponential Growth

5. Al Bartlett, author of “The
Essential Exponential”:
"The greatest shortcoming
of the human race is our
inability to understand the
exponential function“
http://www.albartlett.org/

6. Al Bartlett, author of
“The Essential
Exponential”
Dr. Al Bartlett (1923-2013), a physics professor
at the University of Colorado at Boulder since
1950, dedicated much of his career to educating
the public about the implications of exponential
growth. A video of his presentation “Arithmetic,
Population and Energy” is available online.
http://www.albartlett.org/

7. Growth and
Sustainability: a
Systems Theory
perspective

8. Growth and Sustainability: a
Systems Theory perspective
• What is growth, and why do
we need to think about it?
• What comes to mind when
you think of “growth”?
• Are there limits to growth?

9. The Human system (our material culture,
society, technology, economy) is a
“subsystem of a larger ecosystem that
is finite, non-growing, and materially
closed. The ecosystem is open with
respect to a flow of solar energy, but that
flow is itself finite and non-growing.”
(Herman Daly, a founder of Ecological Economics)
Growth and Sustainability: a
Systems Theory perspective

10. Growth and Sustainability: a
Systems Theory perspective
• We depend on a finite planet.
• We extract material resources (renewable
and nonrenewable).
• We dump waste into the environment.
• We rely on ecosystem services (e. g. clean
water, waste decomposition).
• Human activity is governed and constrained
by the laws of nature (e. g. conservation of
energy, material cycles).

11. The Human system (Anthroposphere) is a
“subsystem of a larger ecosystem that is finite,
non-growing, and materially closed”.
• The Anthroposphere has been expanding for
thousands of years. This expansion is driven by
several factors such as population, consumption
or affluence, and technological change (“I=PAT”
equation).
• A subsystem of a materially closed system
cannot materially grow beyond the limits of the
larger system: an equilibrium must be reached.
Growth and Sustainability: a
Systems Theory perspective

12. The Human Sphere as a Subsystem of
the Ecosphere
Growing
Economic
Subsystem
Recycled
Matter
Energy
Resources
Energy
Resources
Solar
Energy
Waste Heat
Sink
Functions
Source
Functions
Finite Global Ecosystem
(After Robert Costanza,
Gund Institute of Ecological Economics)
Resource consum-
ption and waste
disposal must be in
balance with the
earth’s ecological
capacity.

13. Solar
Energy
Finite Global Ecosystem
Recent history is
characterized by a
dramatic expansion
of the human
“footprint”
Thousands of years ago:
“Empty world” Waste Heat
The Human Sphere as a Subsystem of
the Ecosphere

14. The Human Sphere as a Subsystem of
Planet Earth
Growing
Economic
Subsystem
Recycled
Matter
Energy
Resources
Energy
Resources
Solar
Energy
Waste Heat
Sink
Functions
Source
Functions
Finite Global Ecosystem
Recent history is
characterized by a
dramatic expansion
of the human
“footprint”
Hundreds of years ago?

15. Growing
Economic
Subsystem
Recycled
Matter
Resources
Solar
Energy
Waste Heat
Energy Energy
Resources
Sink
Functions
Source
Functions
Finite Global Ecosystem
Dramatic expansion of
the human footprint:
Humanity takes up an
ever increasing share of
the global ecosystem,
causes planetary scale
environmental change
“Full world”: Have we reached
the limits to growth?
The Human Sphere as a Subsystem of
the Ecosphere

16. Famous 1972 report was an early application
of computer aided systems modeling
The Human Sphere as a Subsystem of
the Ecosphere

17. Ecological Footprint: by current estimates, we
overuse the planet by 50% (footprintnetwork.org)
http://www.footprintnetwork.org/en/index.php/GFN/page/world_footprint/
The Human Sphere as a Subsystem of
the Ecosphere

18. Dimensions of
Growth
How human impact
has multiplied since the
industrial revolution

19. Dimensions of Growth: Raw Materials
Raw material use in US: more than ten-fold
increase since 1900
http://pubs.usgs.gov/annrev/ar-23-107/

20. Dimensions of Growth: Cement Production
World cement production:
50-fold increase since 1926
U.S. Geological Survey Data Series 140

21. Dimensions of Growth: Copper Production
World Copper production:
50-fold increase since 1900
U.S. Geological Survey Data Series 140

22. Dimensions of Growth: Fisheries
Fisheries: six-fold increase since 1950
Source: FAO, 2004. http://earthtrends.wri.org/updates/node/140

23. Dimensions of Growth: Fertilizer
Nitrogen fertilizer: nine-fold increase since 1960
Source: UNEP 2011. https://na.unep.net/geas/getUNEPPageWithArticleIDScript.php?article_id=81

24. Dimensions of Growth: Energy
US electricity consumption: almost ten-fold
increase since 1950
http://www.energyliteracy.com/?p=142

25. Dimensions of Growth: Primary Energy
US primary energy consumption: more than
ten-fold increase since 1900
http://www.theenergysite.info/Markets_Demand.html

26. World primary energy: twenty-fold increase
since 1850, mostly fossil fuels
Dimensions of Growth: Primary Energy

27. World petroleum consumption: more than ten-
fold increase since 1930
Dimensions of Growth: Petroleum
http://www.americanscientist.org/issues/id.6381/issue.aspx

28. World passenger car fleet: more than ten-fold
increase since 1950
Dimensions of Growth: Passenger cars
http://www.mindfully.org/Energy/2003/Americans%20Drive%20Further-May03.htm

29. IMF projects further quadrupling of world wide
car fleet by 2050
Dimensions of Growth: Passenger cars
http://www.planetizen.com/node/41801

30. Dimensions of Growth: Greenhouse gas
emissions
CO2 emissions: Ten-fold increase since 1900

31. Dimensions of Growth: Population
World Population:
from 1 billion in 1800 to 7 billion in 2012
0
1,000,000,000
2,000,000,000
3,000,000,000
4,000,000,000
5,000,000,000
6,000,000,000
7,000,000,000
1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000
Global population since AD 1000

32. Dimensions of Growth: A historical
perspective
• Humans have always manipulated their
environment to extract resources and create
favorable conditions.
• The scale of human impact on the ecosphere has
vastly increased, especially since the industrial
revolution: we are causing planetary scale
environmental change, notably alteration of
atmospheric composition, climate change, alteration
of global material cycles (nitrogen, carbon, water),
mass species extinction, large-scale alteration of
vegetation cover, …

33. Dimensions of Growth: A historical
perspective
• Humans have always manipulated their
environment to extract resources and create
favorable conditions.
• The scale of human impact on the ecosphere has
vastly increased, especially since the industrial
revolution.
• Growth strategies that were successful in an “empty
world” are unsustainable in today’s “full world”.
• Today’s socio-economic institutions are still shaped
by the “growth” paradigm of the past. “Sustainable
growth” has become a buzzword yet it is unclear
what it means.

34. Quantifying growth
Learn how to calculate and
interpret
• Actual (absolute) change
• Fractional (relative) change
• Average rates of change

35. Quantifying growth
Two ways of looking at the growth of a
quantity:
• Actual (absolute) change: by how
many units has the quantity
increased?
• Fractional (relative) change: by
what fraction or percentage has the
quantity increased?

36. Quantifying growth
Absolute change - Example: US
Census
2000: 281.4 million people
2010: 308.7 million people
Increase = 308.7m - 281.4m =
27.3 million people over 10 years

37. Quantifying growth
Relative change - Example: US
Census
2000: 281.4 million people
2010: 308.7 million people
Ratio: Find the solution together with your neighbor
Fractional (percent) increase:
Find the solution together with your neighbor

38. Quantifying growth
Relative change - Example: US
Census
2000: 281.4 million people
2010: 308.7 million people
Factor of increase =
Ratio of final value to initial value =
308.7/ 281.4 = 1.097
Fractional increase:
(ratio-1)*100% = 9.7%

39. Quantifying growth
Note on language use
When the price of a product increases from $10 to $30, we
can say the price has increased by the factor 3 (the ratio of
new price to old price), it has tripled, a three-fold increase,
or it has increased by 200%.
When we refer to a “percent increase” or “fractional
increase”, we always mean the difference between new
value and base value (initial value) divided by the base value:
percent increase =
(new value – base value) / base value*100 =
(new value / base value - 1) * 100.

40. Quantifying growth
Actual versus fractional change
In many contexts, fractional change is the more
useful concept because it allows to quantify
change independently of the base level. Only
so is it meaningful to compare the rate of growth
of different entities (e. g. different countries,
different sectors of the economy). Socio-
economic indicators are often reported as
fractional rates of change: GDP, consumer
spending, the stock market, home prices, tuition
…

41. Quantifying growth
Average Rates of Growth
To make comparison between different time
periods meaningful, growth rates must be
averaged (usually annualized).
Year Population Increase Fractional
increase
1900 76.1 m
2000 281.4 m 205.3 m 170%
2010 308.7 m 27.3 m 9.7%
Example: US Census

42. Quantifying growth
Average Rates of Growth: Absolute
Average yearly increase:
𝒊𝒏𝒄𝒓𝒆𝒂𝒔𝒆 𝒐𝒗𝒆𝒓 𝒕𝒊𝒎𝒆 =
𝒇𝒊𝒏𝒂𝒍 𝒗𝒂𝒍𝒖𝒆 – 𝒃𝒂𝒔𝒆 𝒗𝒂𝒍𝒖𝒆
𝒕𝒊𝒎𝒆
Year Population Increase Avg yearly
increase
1900 76.1 m
2000 281.4 m 205.3 m 2.05 m
2010 308.7 m 27.3 m 2.73 m
Example: US Census

43. Quantifying growth
Average Rates of Growth: Fractional
Average percent growth rate:
𝒈𝒓𝒐𝒘𝒕𝒉 𝒓𝒂𝒕𝒆 =
ln 𝒇𝒊𝒏𝒂𝒍 𝒗𝒂𝒍𝒖𝒆/𝒃𝒂𝒔𝒆 𝒗𝒂𝒍𝒖𝒆
𝒕𝒊𝒎𝒆
× 𝟏𝟎𝟎%
Take the natural logarithm of the ratio (quotient)
between final value and base value, divide by the
number of time units, and multiply by 100.
The average growth rate is measured in inverse time units,
often in percent per year. The annual growth rate is often
denoted p. a. = per annum.

44. Quantifying growth
Average Rates of Growth
Average yearly (annualized) percent growth rate:
𝒈𝒓𝒐𝒘𝒕𝒉 𝒓𝒂𝒕𝒆 =
ln 𝒇𝒊𝒏𝒂𝒍 𝒗𝒂𝒍𝒖𝒆/𝒃𝒂𝒔𝒆 𝒗𝒂𝒍𝒖𝒆
𝒕𝒊𝒎𝒆
× 𝟏𝟎𝟎%
Example: US Census
Year Population in
million
Fractional
increase
Ratio final/
base value
Avg. growth
rate per year
1900 76.1 m
2000 281.4 m 270% 3.70 1.3%
2010 308.7 m 9.7% 1.097 0.9%

45. Quantifying growth
Average Rates of Growth
To make comparison between different time
periods meaningful, growth rates must be
averaged (usually annualized).
Year Population in
million
Avg yearly
increase
Avg. growth
rate per year
1900 76.1 m
2000 281.4 m 2.05 m 1.3%
2010 308.7 m 2.73 m 0.9%
Example: US Census
Why has absolute
growth increased
but fractional
growth declined?

46. Quantifying growth
Example: GDP
U.S. GDP (Gross Domestic Product)
quintupled from $3.1 trillion in 1960 to $15.9
trillion in 2013 (*).
Average growth rate
= ln(15.9 / 3.1)/ 53 *100% = 3.1% p. a.
(p. a. means per annum = per year)
(*) In 2009 chained dollars (adjusted for inflation);
source: U.S. Bureau of Economic Analysis).

47. Quantifying growth
Example: Per capita GDP
US GDP growth 1960-2012: 3.1% p. a.
US population growth 1960-2012:
180m to 314m  1.1% p. a.
Per capita GDP growth:
3.1% - 1.1% = 2.0% p. a.

48. Quantifying growth
Example: Healthcare cost
U.S. National Health Expenditures (NHE)
increased from $307.8 billion in 1970 to
$2,155.9 billion in 2008 (*).
That is a seven-fold increase over 38 years.
Average growth rate
= ln(7) / 38 * 100%= 5.1% p. a.
(*) figures include private and public spending,
adjusted for inflation; source: Health Affairs.

49. Quantifying growth
Example: Primary Energy
Between 1975 and 2012, World
Primary Energy use increased 116%.
Average growth rate
= ln(2.16) / 37 * 100%= 2.1% p. a.
Exercise: Calculate per capita growth
Source: BP Statistical Review of World Energy.

50. Growth models
• Linear growth
• Exponential growth
• Logistic growth

51. Growth models
Linear (arithmetic) growth:
Constant increase per unit of time = straight line

52. The Lily Pond Parable
If a pond lily doubles its leaf
area every day and it takes
30 days to completely cover a
pond, on what day will the
pond be 1/2 covered?
Discuss with your neighbor
Growth models
Exponential (geometric) growth

53. • Exponential (geometric) growth:
Constant fractional (percentage)
increase per unit of time.
• Initially, the population increases
by a small amount per unit of time.
As the population increases, the
increase grows proportionally.
• Exponential growth will eventually
overtake any linear or polynomial
growth function.
Growth models

54. • Linear
• Cubic
• Exponential
Growth models
Exponential (geometric) growth

55. Growth models
Exponential (geometric) growth will eventually
overtake any power (or polynomial) function.
• Cubic
• 10th power
• Exponential

56. Examples of exponential growth:
• Biological reproduction: organisms
reproducing at regular generation
periods will, under favorable condi-
tions, multiply exponentially. Expo-
nential growth in a population occurs
when birth and death rate are
constant, and the former exceeds the
latter.
Growth models

57. Examples of exponential growth:
• Compound interest: the interest paid
on a savings account is a fixed
proportion of the account balance,
compounded in fixed time intervals. If
the real interest rate (corrected for
inflation) remains constant, the account
balance grows exponentially.
Growth models

58. In nature, no sustained material
growth over long time periods has
ever been observed.
→ Natural populations:
Logistic (sigmoid) growth
After an initial phase of
exponential growth, the
growth rate slows as a
threshold (Carrying Capacity)
is approached. Population
may stabilize or decline.
Growth models

59. In nature, no sustained material
growth over long time periods has
ever been observed.
Growth models

60. Learn to understand and apply
• The doubling time
• The Rule of 70
• The power of the powers of 2
• Logarithmic plots
Exponential Growth

61. Continuous exponential growth of a quantity N
over time t at constant fractional rate p is
described by the exponential function
𝑵 𝒕 = 𝑵 𝟎 𝒆 𝒑𝒕 or 𝑵 𝟎exp(𝒑𝒕)
The growth rate can be calculated as
𝒑 =
ln 𝑵(𝒕)/𝑵 𝟎
𝒕
This is the same as the average growth rate
formula introduced earlier. Refer to full
mathematical treatment in the appendix.
Exponential Growth

62. Exponential growth characterized by:
• Constant fractional growth rate
• Doubles in a fixed time period,
called the Doubling Time T2.
• “Rule of 70”: The doubling time
can be estimated by dividing 70 by
the percent growth rate.
(Why? Because 100*ln 2=69.3. Refer to appendix.)
Exponential Growth

63. “Rule of 70”
When steady exponential growth
occurs, the doubling time can be
estimated by dividing 70 by the
percent growth rate p:
𝑻 𝟐 ≈
𝟕𝟎 / 𝒑
Conversely, 𝒑 ≈ 𝟕𝟎 / 𝑻 𝟐
Exponential Growth

64. Doubling Time =
70 over percent
growth rate
Growth
rate in %
1 1.4 2 3 3.5 4 7 10
Doubling
time
70 50 35 23 20 17.5 10 7
Exponential Growth

65. Note on Exponential Decay
Everything said about exponential growth
also applies to exponential decay, where
the “growth” rate is negative. While
sustained exponential growth does not
seem to occur in nature, exponential decay
does: radioactive decay, for example.
Instead of a doubling time, we now refer to
the half-life of a decay process.
Exponential Growth

66. • US population 1900-2010:
Average growth rate 1.3% p.a.
 Doubling time = 70/1.3 = 55 years
• Current US population growth rate 0.8%
 Doubling time = 70/0.8 = 78 years
Doubling in 78 years will occur only IF current
growth rate remains constant!
Doubling time: Examples
Exponential Growth

67. The doubling time can conversely be
used to estimate the growth rate:
• US population quadrupled in 110 years
 Two doublings
 Doubling time = 55 years
 Annual growth rate ≈ 70/55=1.3%
(as calculated before).
Exponential Growth

68. • US economic growth since 1960
averaged 3.1% per year
 Doubling time = 70/3.1 = 23 years
• Health expenditures 1970-2008:
5.1% growth per year
 Doubling time = 14 years
Discuss: Can these trends continue?
Doubling time: Examples
Exponential Growth

69. Health expenditures: 5.1% growth per year
 Doubling time = 14 years!
• What happens when one economic sector grows
faster than the overall economy?
 Health care system share of GDP increased
from 5% in 1960 to 17.2% in 2012
• What happens when a subsystem grows faster
than the overall system? Can the trend continue?
Doubling time: Examples
Exponential Growth

70. Exponential growth implies a
fixed Doubling Time T2. What does
this mean? Example: 7% growth
• 7% yearly growth: T2 = 70/7 = 10 years
• After 10 years: x2 (100% increase)
• After 20 years: x4 (300% increase)
• After 30 years: x8 (700% increase)
• After 40 years: x16 (1,500% increase)
• … How much after 100 years?
Exponential Growth

71. • Exponential growth: doubles in a
fixed time period.
• Doubles again after the next
doubling time.
• After N doubling times have
elapsed, the multiplier is 2 to the
Nth power - 2N!
• 2→4→8→16→32→64→128
→256→512→1024
Exponential Growth

72. The power of the powers of 2
• After N doubling times have elapsed, the
multiplier is 2 to the Nth power - 2N!
2→4→8→16→32→64→
128→256→512→1024 → …
• The 10th power of 2 is approx. 1,000.
• The 20th power of 2 is approx. 1,000,000.
• The 30th power of 2 is approx. 1,000,000,000.
Exponential Growth

73. Exercise: how many doublings has the human
population undergone?
Make a guess!
Try to estimate:
• Initial population: minimum 2 (not to be taken literally)
• Current population: 7 billion
• 1 billion is about … doublings
• Fill in the details.
The power of the powers of 2
Exponential Growth

74. Exercise: how many doublings has the human
population undergone?
Estimate:
• Initial population: minimum 2 (not to be taken literally)
• Current population: 7 billion
• 1 billion is about 30 doublings
• 2x2x2=8
Answer: at most 32 doublings.
• What did you guess?
• How many more doublings can the earth support?
The power of the powers of 2
Exponential Growth

75. Growth over a life time
A human life span is roughly 70 years. What are
the consequences of 70 years of steady growth at
an annual rate p%?
The doubling time is T2 =70/p, so exactly p
doublings will be observed.
So the multiplier over 70 years is 2p.
The power of the powers of 2
Exponential Growth

76. Growth over a life time
A human life span is about 70 years. What are the
consequences of 70 years of steady growth at an
annual rate p%? The multiplier over 70 years is 2p
.
Example p=3%: Multiply by 23
= 8.
3% per year is often considered a moderate rate of
growth (e. g. in terms of desired economic growth)
yet it amounts to a tremendous 700% increase
within a human life span.
The power of the powers of 2
Exponential Growth

77. Exercise: The consequences of 3.5% p. a.
steady exponential growth
• What is the doubling time?
• How long will it take to increase four-fold, sixteen-fold.
1000-fold?
• Make a guess first, then work it out using the rule of 70!
The power of the powers of 2
Exponential Growth

78. The consequences of a 3.5% growth rate:
• Doubling time: T2 = 20 years
• 200 years = 10 x T2 corresponds to a multiplier of 1000.
• 200 years may seem long from an individual perspective
but is a short period in history.
• 200 years is less than the history of industrial society,
and less than the age of the United States.
• The Roman Empire lasted about 700 years.
• Sustainability is sometimes defined as the imperative to
“think seven generations ahead” – about 200 years - in
the decisions we make today.
The power of the powers of 2
Exponential Growth

79. The consequences of a 3.5% growth rate:
• Doubling time: T2 = 20 years
• 200 years = 10 x T2 corresponds to a multiplier of 1000.
Some economic models assume a long term growth rate
on the order of 3-4% p.a.. Can you imagine the economic
system to grow 1000 fold? What would that mean?
• 1000 times the cars, roads, houses, airports, sewage
treatment plants, factories, power plants?
• 1000 times the resource use and pollution?
• What is it that could/would/should grow 1000 times?
The power of the powers of 2
Exponential Growth

80. The consequences of 3.5% yearly growth:
• Doubling time: T2 = 20 years
• 200 years = 10 x T2 corresponds to a multiplier of 1000.
 Our difficulty in grasping the long term
consequences of seemingly “low” to “moderate”
exponential growth is what Al Bartlett referred to
as humanity’s “greatest shortcoming”.
The power of the powers of 2
Exponential Growth

81. Caution!
Extrapolating current growth trends into the
future (for example using doubling times) is
usually not permissible because trends change
over time. Doubling times are only indicative of
what would happen if the trend continued. It
would be questionable to base policy decisions
on such trends – although this is often done.
Example: Population growth rates have changed
dramatically over time.
Exponential Growth

82. How can we recognize exponential
growth in a time series?
• Inspect the data?
• Analyze the data?
• Inspect the graph?
Exponential Growth

83. How can we recognize exponential
growth in a time series?
• Inspect the data
Example: Census population of Georgia
This data series is roughly consistent with
exponential growth, doubling time 35-40 years.
Year 1960 1970 1980 1990 2000 2010
Pop. inmillion 3.9 4.6 5.4 6.5 8.2 9.7
Year 1960 1970 1980 1990 2000 2010
Population
in million
3.9 4.6 5.4 6.5 8.2 9.7
Exponential Growth

84. How can we recognize exponential
growth in a time series?
• Analyze the data
Example: Census population of Georgia
Fractional growth rates are fairly consistent, with the
1990s somewhat higher.
Year 1960 1970 1980 1990 2000 2010
Pop. inmillion 3.9 4.6 5.4 6.5 8.2 9.7
Year 1960 1970 1980 1990 2000 2010
Population
in million
3.9 4.6 5.4 6.5 8.2 9.7
% increase 18% 17% 20% 26% 18%
Exponential Growth

85. How can we recognize exponential
growth in a time series?
• Inspect the graph?
Caution! It is difficult to judge growth rates
from the appearance of a graph.
Example: population growth
Exponential Growth

86. 0
1,000,000,000
2,000,000,000
3,000,000,000
4,000,000,000
5,000,000,000
6,000,000,000
7,000,000,000
1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000
Global population since AD 1000
Steady exponential growth?
Population Growth

87. 0
0.5
1
1.5
2
1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000
Global population fractional growth rates, AD
1000 to present
Steady exponential growth? No. Growth
rates have changed dramatically over time!
Population Growth

88. How can we recognize exponential
growth in a time series?
• Inspect the graph?
We need to plot the data to logarithmic
scale. This makes an exponential function
appear as a straight line. The slope
corresponds to the growth rate.
The Logarithmic Scale

89. The semi-logarithmic plot makes an exponential function
appear as a straight line (red line). The slope corresponds
to the growth rate. A function that grows slower than
exponential gives a concave graph (green line).
It is easy to
change to
logarithmic
scale in a
spreadsheet
software.
The Logarithmic Scale

90. Example: Global Population
The slope in a
semi-logarithmic
plot corresponds
to the growth
rate.
Can you identify
distinct phases
of population
growth?
The Logarithmic Scale

91. Population growth
accelerated with the
onset of the industrial
revolution and reached
a peak about 1970.
Population growth was
hyper- (faster than)
exponential in that
period (evident in the
semi-logarithmic graph
being convex ).
Since 1970, the rate of
growth is in decline but
still exceptionally high
by historical standards.
The Logarithmic Scale

92. In a semi-logarithmic plot, the slope corresponds to the
growth rate.
Example: Primary Energy Use since 1975
Here, a trend line
was fitted to show
that the data are
consistent with
exponential growth
at about 2.% p. a.
Data source: BP Statistical Review of World Energy
The Logarithmic Scale

93. In a semi-logarithmic plot, the slope corresponds to the
growth rate.
Example: Economic Growth since 1970
North America,
East Asia, World
Where are growth
rates highest?
Are data consistent
with exponential
growth (straight
line)? Are trends
changing?
Plotted logarithmically using the Google Public Data explorer
The Logarithmic Scale

94. Which of our case studies exhibit
sustained exponential growth?
• Global Population: no, growth rates are falling
and stabilization is expected by mid or late 21st
century
• Global Energy Use: yes, 2% p. a.
• Global Economic Output: yes, 3% p. a.
• Trends are regionally very different – see
following exercise!
The Logarithmic Scale

95. Exercise: Use the Google Public Data Explorer
Go to www.google.com/publicdata/explore?ds=d5bncppjof8f9_. You are
now on an interactive interface which with you can explore the World
Development Indicators, a wealth of data compiled by the World Bank
for the last 50 years or so. Find data on the thematic menu on the left or
by typing a key word into the search box. Once you have selected a
data series, you can choose for which countries or regions you want it
displayed. You can choose between different
chart types (line chart, bar chart, map chart,
bubble chart) on the task bar:
Spend some time to familiarize yourself with
the data explorer the interface. Look for interesting data sets, try
out the different chart types, especially the
bubble chart, and find out something you always wanted to know.
The Logarithmic Scale

96. Exercise: Use the Google Public Data Explorer
Look up some data sets such as population, energy use, cereal
production, Gross National Income (GNI, in constant 2000$). For
each, look up the world-wide numbers. Examine how they changed
over time. Try to visualize the magnitude of the numbers. Compare
the data for your own and selected other countries and regions. For
some indicators, you can examine both the per capita and the
aggregate values. For each indicator, read and understand the
definition. Understand the units in which each is measured.
Plot the data to linear and logarithmic scale.
Calculate and compare growth rates. For
example, how do energy use or cereal production
compare with population growth? Identify
exponential growth. Use all the techniques you
have learned to explore relevant real world data!
The Logarithmic Scale

97. • Exponential growth is characterized by a constant growth
rate and doubling time.
• Rule of 70:
Doubling Time = 70 over percent growth rate
• Logarithmic plots make growth rates visible.
• Knowing growth rates and doubling times helps better
understand environmental, social, and economic
challenges.
• Exponential growth becomes unsustainable very quickly.
In the real world, exponential growth processes are
unusual and don’t last long.
Summary

98. • Al Bartlett (1993): Arithmetic of Growth
• Herman E. Daly (1997): Beyond Growth: The
Economics of Sustainable Development
• Herman E. Daly (2012): Eight Fallacies about Growth
• Charles A. S. Hall and John W. Day, Jr. (2009):
Revisiting the Limits to Growth After Peak Oil
• Richard Heinberg (2011): The End of Growth:
Adapting to Our New Economic Reality
• Tim Jackson (2011): Prosperity Without Growth:
Economics for a Finite Planet
• Toni Menninger (2014): Exponential Growth, Doubling
Time, and the Rule of 70
• Tom Murphy (2011): Galactic-Scale Energy, Do the
Math
Further readings

99. Growth in a Finite World
Sustainability and the Exponential Function
This presentation is part of the Lecture Series in Sustainability
Science. © 4/2014 by Toni Menninger MSc. Use of this material for
educational purposes with attribution permitted. Questions or
comments please email toni.menninger@gmail.com.
Related lectures and problem sets available at
http://www.slideshare.net/amenning/presentations/:
• The Human Population Challenge
• Energy Sustainability
• World Hunger and Food Security
• Economics and Ecology
• Exponential Growth, Doubling Time, and the Rule of 70
• Case Studies and Practice Problems for Sustainability Education:
• Agricultural Productivity, Food Security, and Biofuels
• Growth and Sustainability
… and more to come!

100. Appendix:
The Mathematics of
Exponential Growth

101. Mathematics of Exponential Growth
A quantity is said to grow exponentially at a constant (steady) rate if it increases by
a fixed percentage per unit of time. In other words, the increase per unit of time is
proportional to the quantity itself, in contrast with other types of growth (e. g.
arithmetic, logistic). Geometric growth is another word for exponential growth.
Examples
• Compound interest: the interest is a fixed proportion of the account balance,
compounded in fixed time intervals (years, months, days). One can imagine the
interval becoming smaller and smaller until interest is added continuously. This is
known as continuous compounding.
• Biological reproduction: cells dividing at regular time intervals, organisms
reproducing at regular generation periods will, under favorable conditions,
multiply exponentially. Exponential growth in a population occurs when birth and
death rate are constant, and the former exceeds the latter.
• Economics: economic output is often assumed to grow exponentially because
productive capacity roughly depends on the size of the economy. Current
macroeconomic models do not incorporate resource constraints.
• The inverse process is known as exponential decay (e. g. radioactive decay), or
“negative growth”.

102. Mathematics of Exponential Growth
We introduce
N : a quantity, e. g. a population count, an amount of money, or a rate of
production or resource use
N0 : the initial value of N
p : the rate of growth per unit of time, as a decimal
p% : the rate of growth as a percentage (=100 p)
t : the time period in units of time, e. g. in days or years
N(t) : the value of N after time t has elapsed.
Assume a savings account with an initial deposit of $100 carries 6% interest
compounded annually. Then N0 = $100, p = 0.06, p%= 6, and N(15) would be the
amount accumulated after 15 years (if left untouched and the interest rate remains
constant).
The first year earns $6 interest, so 𝑵 𝟏 = $𝟏𝟎𝟎 + $𝟔 = $𝟏𝟎𝟔 = $𝟏𝟎𝟎 × 𝟏. 𝟎𝟔.
The second year, we have 𝑵 𝟐 = $𝟏𝟎𝟔 × 𝟏. 𝟎𝟔 = $𝟏𝟎𝟎 × 𝟏. 𝟎𝟔𝟐 .
After t years, 𝑵 𝒕 = $𝟏𝟎𝟎 × 𝟏. 𝟎𝟔𝒕.

103. Mathematics of Exponential Growth
The exponential growth equation
The general formula for discrete compounding is:
𝑵 𝒕 = 𝑵 𝟎 (𝟏 + 𝒑) 𝒕
.
In most real world situations, variables like population don’t make discrete jumps (e.
g. once a year) but grow continuously. Continuous compounding is described by
the exponential function:
𝑵 𝒕 = 𝑵 𝟎 𝒆 𝒑𝒕
or 𝑵 𝒕 = 𝑵 𝟎 𝒆𝒙𝒑(𝒑𝒕)
where e = 2.718… is the base of the natural logarithm. In practice, both formulas
give approximately the same results for small growth rates but the continuous
growth model is preferable to discrete compounding because it is both more realistic
and mathematically more convenient.
The exponential growth formula contains three variables. Whenever two of them are
known, the third can be calculated using simple formulas. Often, one is interested
more in the relative growth 𝑵(𝒕)/𝑵 𝟎 than in the absolute value of N(t). In that case,
one can get rid of 𝑵 𝟎 by setting 𝑵 𝟎 =1=100%.

104. Mathematics of Exponential Growth
Solving the exponential growth equation
𝑵 𝒕 = 𝑵 𝟎 𝒆 𝒑𝒕
Case 1: A quantity is growing at a known growth rate for a known period of time, by
what factor does it grow? Answer:
𝑵 𝒕
𝑵 𝟎
= 𝒆 𝒑𝒕
Case 2: A quantity grows at a known rate p. After what period of time has it grown
by a given factor? The equation is solved by taking the natural logarithm (written ln)
on both sides. Answer:
𝒍𝒏( 𝑵(𝒕)/𝑵 𝟎) = 𝒑𝒕 → 𝒕 =
𝒍𝒏(𝑵(𝒕)/𝑵 𝟎)
𝒑
Case 3: In a known period of time, a quantity increases by a known factor. Find the
(average) growth rate.
Answer:
𝒑 =
𝐥𝐧( 𝑵(𝒕)/𝑵 𝟎)
𝒕
=
𝒍𝒏 𝑵 𝒕 − 𝐥𝐧 𝑵 𝟎
𝒕

105. Mathematics of Exponential Growth
The doubling time and rule of 70
To grasp the power of the exponential growth process, consider that if it doubles
within a certain time period, it will double again after the same period. And again and
again. The doubling time, denoted T2, can be calculated using equation (4) by
substituting
𝑵 𝒕
𝑵 𝟎
= 𝟐 → 𝑻 𝟐 =
𝐥𝐧( 𝟐)
𝒑
=
𝟎. 𝟔𝟗𝟑
𝒑
=
𝟔𝟗. 𝟑
𝟏𝟎𝟎 𝒑
A convenient approximation is
𝑻 𝟐 ≈
𝟕𝟎
𝒑%
Thus, the doubling time of an exponential growth process can be estimated by
dividing 70 by the percentage growth rate. This is known as the “rule of 70” and
allows estimating the consequences of exponential growth with little effort.

106. Mathematics of Exponential Growth
Thousand-fold increase
Knowing the doubling time, it follows that after twice that period, the increase is
fourfold; after three times the doubling time, eightfold. After 𝑡 = 𝑛 × 𝑇2 time units, n
doublings will have been observed, giving a multiplication factor of 2n. It is
convenient to remember 210
= 1024 ≈ 1000 = 103
. After ten doubling times,
exponential growth will have exceeded a factor of 1000:
𝑻 𝟏𝟎𝟎𝟎 ≈ 𝟏𝟎 × 𝑻 𝟐 ≈
𝟕𝟎𝟎
𝒑%
For a 7% growth rate, the doubling time is a decade and the time of thousand-
fold increase is a century.
Growth over a life time
A human life span is roughly 70 years. What are the consequences of 70 years of
steady growth at an annual rate p? From 𝑇2 ≈
70
𝑝%
follows that 70 years
encompass almost exactly p% doubling times and the total aggregate growth will be
𝑵(𝒕)
𝑵 𝟎
≈ 𝟐 𝒑%
This is another convenient rule to remember.

107. Mathematics of Exponential Growth
Per capita growth
If two time series Q(t) and N(t) both follow an exponential growth pattern with
growth rates q and p, then the quotient also grows or contracts exponentially. The
growth rate is simply the difference of the growth rates, and Q(t)/N(t) grows if
𝒒 − 𝒑 > 𝟎:
𝑸 𝒕 = 𝒆 𝒒𝒕
, 𝑵 𝒕 = 𝒆 𝒑𝒕
→
𝑸 𝒕
𝑵 𝒕
= 𝒆 𝒒−𝒑 𝒕
A typical application is per capita growth, where N is a population and Q might be
energy use or economic output. Q could also indicate a subset of N, for example a
sector of the economy, and Q/N would indicate Q as a share of the total economy.
Cumulative sum of exponential growth
If a rate of resource use R(t), such as the rate of energy use, grows exponentially,
then the cumulative resource consumption also grows at least exponentially. During
each doubling time, the aggregate resource use is twice that of the preceding
doubling time, and at least as much of the resource is used as has been used
during the entire prior history. A startling fact to consider!

108. Mathematics of Exponential Growth
Summary table
A few simple rules, especially the rule of 70, are often sufficient to get a good
estimate of the effects of growth. The following table summarizes the results for a
range of growth rates.
Semi-logarithmic graphs
For a given time series, it is not usually obvious whether it belongs to an exponential
process. A semi-logarithmic plot helps to visually assess its growth characteristics.
Steady exponential growth will show as a straight line on the graph. Line segments
of different slope indicate a change in growth rates.
For full mathematical treatment, see: Exponential Growth, Doubling Time, and the Rule of 70
Growth rate in % 0.5 1 1.4 2 3 3.5 4 5 7 10
Doubling time T2 140 70 50 35 23 20 17.5 14 10 7
Growth per 70 years 1.4 2 2.6 4 8 11.3 16 32 128 1024
T1000 1400 700 500 350 233 200 175 140 100 70