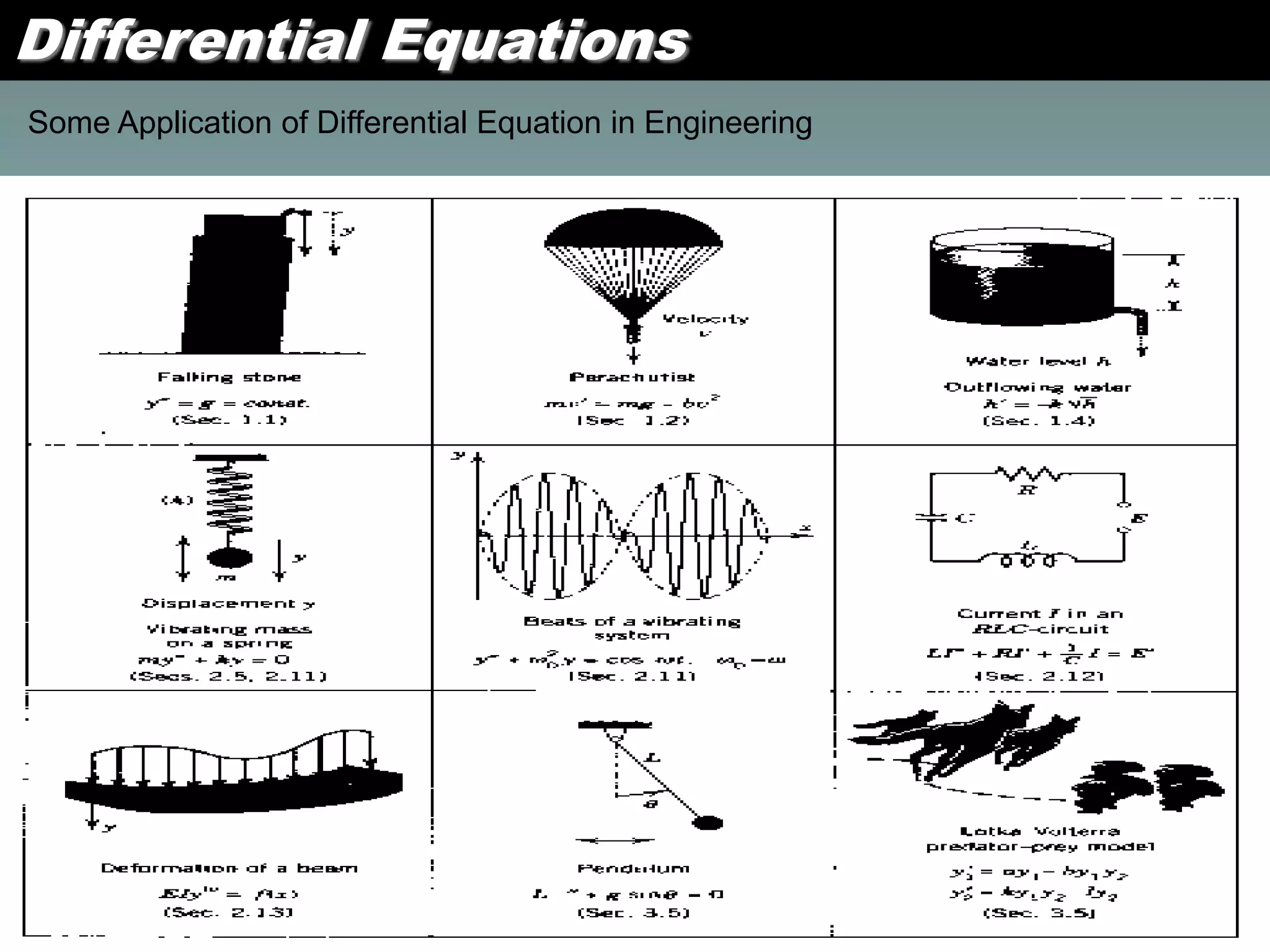
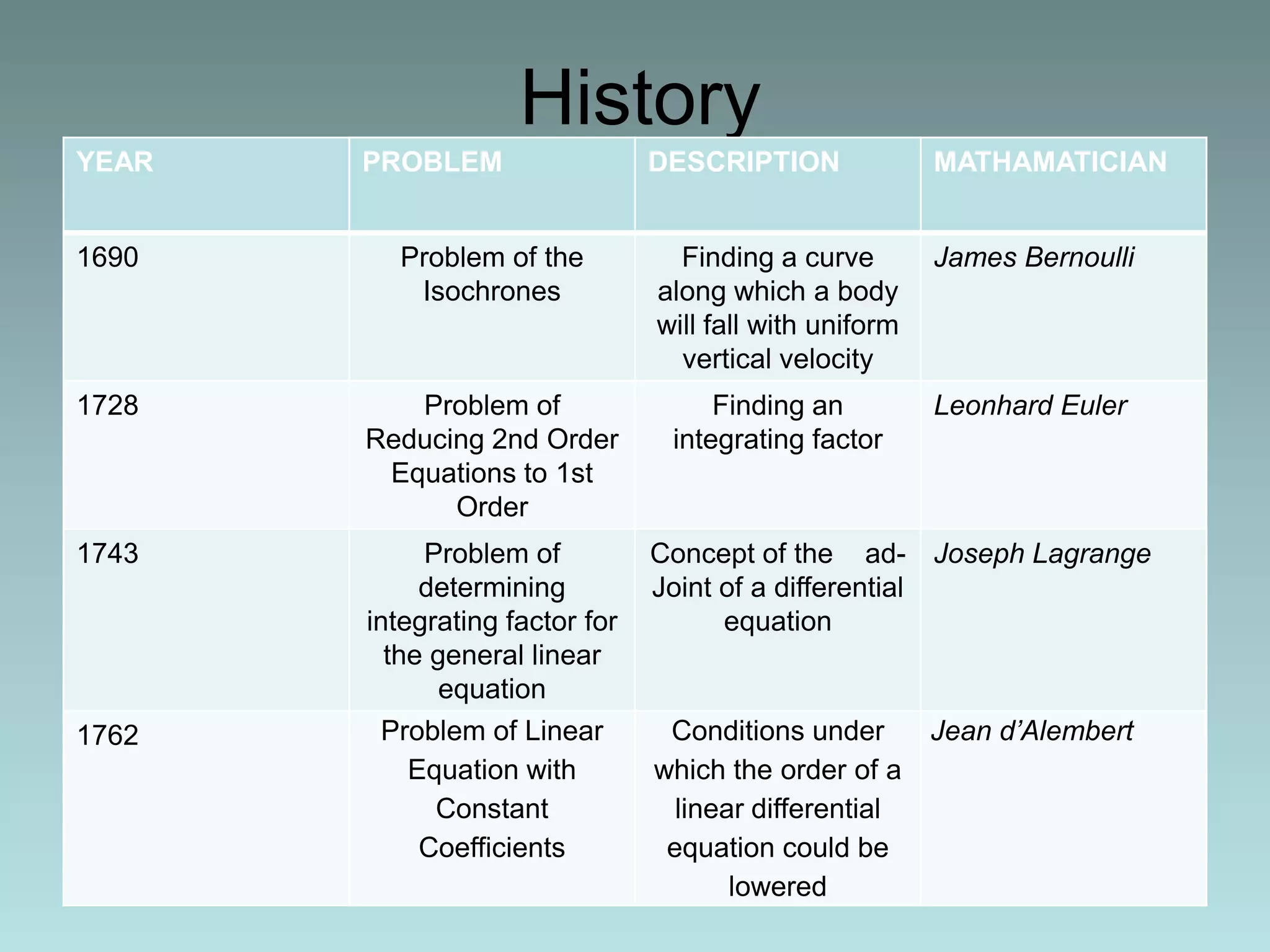
1. A differential equation relates an unknown function and its derivatives, and can be ordinary (involving one variable) or partial (involving partial derivatives).
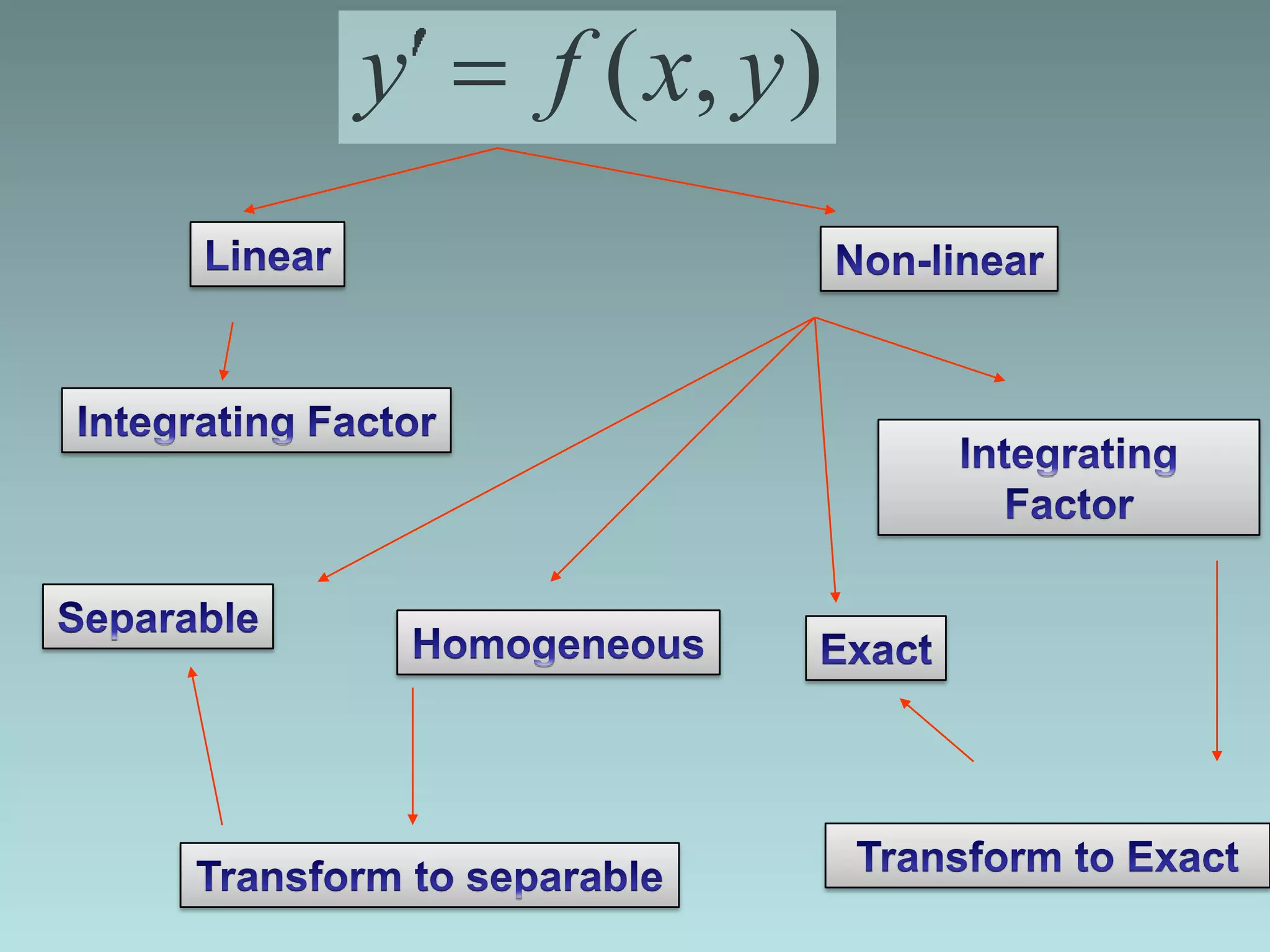
2. Linear differential equations have dependent variables and derivatives that are of degree one, and coefficients that do not depend on the dependent variable.
3. Common methods for solving first-order linear differential equations include separation of variables, homogeneous equations, and exact equations.